-
Find the additive inverse of the matrix \[A=\left[ \begin{matrix} 2 & -\,5 & 0 \\ 4 & 3 & -\,1 \\ \end{matrix} \right]\]
View Answer play_arrow
-
What are the direction cosines of a line which makes equal angles with the coordinate axes?
View Answer play_arrow
-
A ladder 5 m long, standing on a horizontal floor, leans against a vertical wall. If the two of the ladder slides downwards at the rate of 10 cm/s, then find the rate at which the angle between the floor and ladder is decreasing when the lower end of ladder is 2 m from the wall.
View Answer play_arrow
-
Evaluate \[\int{{{e}^{ax}}\{af(x)+f'(x)\}\,dx.}\]
View Answer play_arrow
-
Evaluate \[\int{\frac{{{x}^{3}}}{{{x}^{4}}+3{{x}^{2}}+2}}\,dx.\]
View Answer play_arrow
-
Find the values of \[\lambda \] and \[\mu \] for which \[(2\hat{i}+6\hat{j}+27\hat{k})\times (\hat{i}+\lambda \hat{j}+\mu \hat{k})=\vec{0}\]
View Answer play_arrow
-
If\[f(x)=\left\{ \begin{matrix} \frac{{{\cos }^{2}}x-{{\sin }^{2}}x-1}{\sqrt{{{x}^{2}}+1}-1}, & x\ne 0 \\ a, & x=0 \\ \end{matrix} \right.\] is continuous at x = 0, find the value of a.
View Answer play_arrow
-
Prove that the determinant
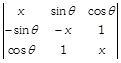
is independent of \[\theta .\]
-
If \[f(x)={{x}^{3}}+a{{x}^{2}}+bx+c\] has maximum value at \[x=-1\] and minimum at x = 3. Determine the values of a, b and c.
View Answer play_arrow
-
If \[y=\frac{{{5}^{x}}}{{{x}^{5}}},\] then find \[\frac{dy}{dx}.\]
View Answer play_arrow
-
Find the approximate value of \[{{(1.999)}^{5}}.\]
View Answer play_arrow
-
If \[A=\left[ \begin{matrix} x & 0 \\ 1 & 1 \\ \end{matrix} \right]\] and \[B=\left[ \begin{matrix} 1 & 0 \\ 5 & 1 \\ \end{matrix} \right],\] then find the value of x for which \[{{A}^{2}}=B.\]
View Answer play_arrow
-
Prove that \[{{\tan }^{-1}}\left[ \frac{\sqrt{1+{{x}^{2}}}+\sqrt{1-{{x}^{2}}}}{\sqrt{1+{{x}^{2}}-\sqrt{1+{{x}^{2}}}}} \right]=\frac{\pi }{4}+\frac{1}{2}{{\cos }^{-1}}{{x}^{2}}\]
View Answer play_arrow
-
Show that x = 2 is a root of the equation formed by the following determinant.
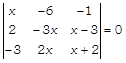
Hence, solve the equation.
-
If \[y={{a}^{{{x}^{{{a}^{x...\infty }}}}}},\] prove that \[\frac{dy}{dx}=\frac{{{y}^{2}}\log \,\,y}{x[1-y\log \,x\log \,y]}.\]
View Answer play_arrow
-
| Evaluate \[\int{\left[ \log (\log \,x)+\frac{1}{{{(\log \,x)}^{2}}} \right]}\,dx.\] |
| OR |
| Evaluate \[\int{\frac{\cos 2x-\cos 2\alpha }{\cos x-\cos \alpha }}\,dx.\] |
View Answer play_arrow
-
Evaluate the integral \[\int{\frac{{{\sin }^{-1}}\sqrt{x}-{{\cos }^{-1}}\sqrt{x}}{{{\sin }^{-1}}\sqrt{x}+{{\cos }^{-1}}\sqrt{x}}\,dx.}\]
View Answer play_arrow
-
Solve the differential equation \[(x\,dy-y\,dx)\,\,y\,\,\sin \left( \frac{y}{x} \right)\] \[-(y\,\,dx+x\,\,dy)\,x\,\,\cos \left( \frac{y}{x} \right)=0.\]
View Answer play_arrow
-
Solve the differential equation \[\left( \frac{{{e}^{-2\sqrt{x}}}}{\sqrt{x}}-\frac{y}{\sqrt{x}} \right)\,\,\frac{dx}{dy}=1,\] \[x\ne 0.\]
View Answer play_arrow
-
Express the vector \[\vec{a}=(5\hat{i}\,-2\hat{j}\,+5\hat{k})\] as sum of two vectors such that one is parallel to the vector \[\vec{b}=(3\hat{i}\,+\hat{k})\] and the other is perpendicular to \[\vec{b}.\]
View Answer play_arrow
-
| Find the angle between the line |
| \[\frac{x+1}{2}=\frac{y}{3}=\frac{z-3}{6}\] and the plane \[10x+2y-11z=3.\] |
| OR |
| Find the equation of the plane which contains the line of intersection of |
| planes \[\vec{r}\cdot (\hat{i}+2\hat{j}+3\hat{k})-4=0,\] |
| \[\vec{r}\cdot (2\hat{i}+\hat{j}+\hat{k})-15=0\] and is perpendicular to the plane |
| \[\vec{r}\cdot (5\hat{i}+3\hat{j}-6\hat{k})+8=0.\] |
View Answer play_arrow
-
| It is known that 10% of certain articles manufactured are defective. What is probability that in a random sample such articles, 9 are defective? |
| OR |
| Consider the experiment of tossing a coin. If the coin shows tail, toss it again but if it shows head, then throw a die. Find the conditional probability off event that 'the die shows a number greater than 3' given that 'there is at least one head'. |
View Answer play_arrow
-
To promote the making of toilets for women, an organisation tried to generate awareness through (i) house calls (ii) letters (iii) announcements. The cost for each mode per attempt is given below (i) Rs. 50 (ii) Rs. 20 (iii) Rs. 40 The number of attempts made in three villages X, Y and Z are given below
| Villages | House calls | Letters | Announcements |
| X | 400 | 300 | 100 |
| Y | 300 | 250 | 75 |
| Z | 500 | 400 | 150 |
Find the total cost incurred by the organisation for X and Z villages separately using matrices. Write one value generated by the organisation in the society.
-
| If \[f:R-\{2\}\to R-\{3\}\] is defined by |
| \[f(x)=\frac{3x+1}{x-2},\] where R is the set of real numbers, |
| show that f is invertible and hence find the value of \[{{f}^{-1}}.\] |
| OR |
| Let \[f:N\to R\] be a function defined as \[f(x)=4{{x}^{2}}+12x+15.\] Show that \[f:N\to \] range f is invertible. Find the inverse of \[{{f}^{-1}}\]. |
View Answer play_arrow
-
| A point on the hypotenuse of a right angled triangle is at distance of a units and b units from the sides. Show that the minimum length of hypotenuse is \[{{({{a}^{2/3}}+{{b}^{2/3}})}^{3/2}}.\] |
| OR |
| If the straight line \[x\cos \alpha +y\sin \alpha =P\] touches the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1,\] prove that \[{{P}^{2}}={{a}^{2}}{{\cos }^{2}}\alpha +{{b}^{2}}{{\sin }^{2}}\alpha .\] |
View Answer play_arrow
-
A farmer has a supply of chemical fertilizers of type A which contains 10% nitrogen and 6% phosphoric acid and type B contains 5% of nitrogen and 10% of phosphoric acid. After soil testing, it is found that at least 7 kg of nitrogen and same quantity of phosphoric acid is required for a good crop. The fertilizers of types A and B cost Rs. 5 and Rs. 8 per kg, respectively. By using LPF; find how many kilograms of each type of fertilizers should be bought to meet the requirement and cost be minimum? Solve the problem graphically. We generally deal with two types of farming (i) Farming using fertilizers (ii) Organic farming Which farming you would perfer and why?
View Answer play_arrow
-
| Find the image of the point \[2\hat{i}+3\hat{j}-4\hat{k}\] in the plane \[\vec{r}\cdot (2\hat{i}-\hat{j}+\hat{k})=3.\] |
| OR |
| Find the equation of the plane through the line of intersection of the planes \[x+y+z=1\] and \[2x+3y+4z=5,\] which is perpendicular to the plane \[x-y+z=0.\] Also, find the distance of the plane obtained above from the point (1, 1, 1). |
View Answer play_arrow
-
Find the area lying above the X-axis and included between the circle \[{{x}^{2}}+{{y}^{2}}=8x\] and parabola \[{{y}^{2}}=4x.\]
View Answer play_arrow
-
Let \[{{d}_{1}},\] \[{{d}_{2}}\] and \[{{d}_{3}}\] be three mutually exclusive diseases and \[S=({{s}_{1}},\,{{s}_{2}},\,{{s}_{3}},....,{{s}_{6}})\] be the set of observable symptoms of these disease. For example, \[{{s}_{1}}\] is the shortness of breath, \[{{s}_{2}}\] is loss of weight, \[{{s}_{3}}\] is fatigue, etc. Suppose a random sample of 10000 patients contains 3200 patients with disease \[{{d}_{1}},\] 3500 with disease \[{{d}_{2}}\] and 3000 with disease \[{{d}_{3}}\] Also, 3100 patients with disease \[{{d}_{1}},\] 3300 with disease \[{{d}_{2}}\] and 3000 with disease \[{{d}_{3}}\] show the symptoms S. Knowing that the patient has symptom S, the doctor wishes to determine the patient's illness. On the basis of this information, what should the doctor conclude?
View Answer play_arrow
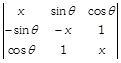 is independent of \[\theta .\]
is independent of \[\theta .\] 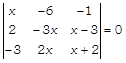 Hence, solve the equation.
Hence, solve the equation. 