question_answer

A point on the hypotenuse of a right angled triangle is at distance of a units and b units from the sides. Show that the minimum length of hypotenuse is \[{{({{a}^{2/3}}+{{b}^{2/3}})}^{3/2}}.\]

OR

If the straight line \[x\cos \alpha +y\sin \alpha =P\] touches the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1,\] prove that \[{{P}^{2}}={{a}^{2}}{{\cos }^{2}}\alpha +{{b}^{2}}{{\sin }^{2}}\alpha .\]

Answer:

Let AOB be a right triangle with hypotenuse AB such that a point P on AB is distance a and b from OA and OB respectively i.e. PL = a and PM = b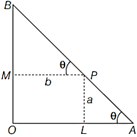

Let \[\angle OAB=\theta \]

Then,\[AP=a\cos ec\,\theta \]\[BP=b\sec \theta \]

Let ?l? be the length of the hypotenuse AB. Then,

\[l=AP+BP\Rightarrow l=a\cos ec\theta +b\sec \theta \]

\[\Rightarrow \]   \[\frac{dl}{d\theta }=-\,a\cos ec\theta \cot \theta +b\sec \theta \tan \theta \]

and       \[\frac{{{d}^{2}}l}{d{{\theta }^{2}}}=a\cos e{{c}^{3}}\theta +a\cos ec\theta {{\cot }^{2}}\theta \]

\[+b{{\sec }^{2}}\theta +b\sec \theta {{\tan }^{2}}\theta \]

For maximum or minimum, put

\[\frac{dl}{d\theta }=0\]

\[-\,a\cos ec\theta \cot \theta +b\sec \theta \tan \theta =0\]

\[\Rightarrow \]   \[-\,a\frac{\cos \theta }{{{\sin }^{2}}\theta }+\frac{b\sin \theta }{{{\cos }^{2}}\theta }=0\]\[\Rightarrow \]\[{{\tan }^{3}}\theta =\frac{a}{b}\]

\[\Rightarrow \]   \[\tan \theta ={{\left( \frac{a}{b} \right)}^{1/3}}\]

\[\therefore \]\[\sin \theta =\frac{{{a}^{1/3}}}{\sqrt{{{a}^{2/3}}}+{{b}^{2/3}}}\]and \[\cos \theta =\frac{{{b}^{1/3}}}{\sqrt{{{a}^{2/3}}}+{{b}^{2/3}}}\]

Clearly, \[\frac{{{d}^{2}}l}{d{{\theta }^{2}}}>0\]for\[\tan \theta ={{\left( \frac{a}{b} \right)}^{1/3}}\]

Thus, l is minimum, when \[\tan \theta ={{\left( \frac{a}{b} \right)}^{1/3}}\]

The minimum value of l is given by

\[l=a\cos ec\theta +b\sec \theta \]

\[l=a\sqrt{1+\cot 2\theta }+b\sqrt{1+{{\tan }^{2}}\theta }\]

\[\Rightarrow \]   \[l=a\sqrt{1+{{\left( \frac{b}{a} \right)}^{2/3}}}+b\sqrt{1+{{\left( \frac{a}{b} \right)}^{2/3}}}\]

\[\Rightarrow \]   \[\lambda ={{({{a}^{2/3}}+{{b}^{2/3}})}^{3/2}}\]

OR

Let the point P (h, k) lie on the curve

\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]

On differentiating w.r.t. x, we get

\[\frac{2x}{{{a}^{2}}}+\frac{2y}{{{b}^{2}}}\frac{dy}{dx}=0\Rightarrow \frac{dy}{dx}=\frac{-\,{{b}^{2}}y}{{{a}^{2}}y}\]

\[\Rightarrow \]   \[{{\left( \frac{dy}{dx} \right)}_{h,\,\,k}}=-\frac{{{b}^{2}}y}{{{a}^{2}}k}\]

Since,\[x\cos \alpha +y\sin \alpha =P\]is a tangent of curve.

\[\therefore \]Point P (h, k) lie on the tangent

\[x\cos \alpha +y\sin \alpha =P\]

\[\Rightarrow \]   \[h\cos \alpha +k\sin \alpha =P\]                 ?(i)

Slope of tangent of curve = Slope of tangent of

\[x\cos \alpha +y\sin \alpha =P\]

\[\therefore \]      \[\frac{-\,{{b}^{2}}h}{{{a}^{2}}k}=-\frac{\cos \alpha }{\sin \alpha }\]

\[\Rightarrow \]   \[h=\frac{{{a}^{2}}\cos \alpha k}{{{b}^{2}}\sin \alpha }\]

On putting the value of h in Eq. (i), we get

\[\frac{{{a}^{2}}{{\cos }^{2}}\alpha k}{{{b}^{2}}\sin \alpha }+k\sin \alpha =P\]

\[\Rightarrow \]   \[k=\frac{P{{b}^{2}}\sin \alpha }{{{a}^{2}}{{\cos }^{2}}\alpha +{{h}^{2}}{{\sin }^{2}}\alpha }\]

and       \[h=\frac{P{{a}^{2}}\cos \alpha }{{{a}^{2}}{{\cos }^{2}}\alpha +{{b}^{2}}{{\sin }^{2}}\alpha }\]

On putting the value of (h, k) in equation of curve

\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1,\] we get

\[\frac{{{P}^{2}}{{a}^{4}}{{\cos }^{2}}\alpha }{a\,{{({{a}^{2}}{{\cos }^{2}}\alpha +{{b}^{2}}{{\sin }^{2}}\alpha )}^{2}}}+\frac{{{P}^{2}}{{b}^{4}}{{\sin }^{2}}\alpha }{{{b}^{2}}({{a}^{2}}{{\cos }^{2}}\alpha +{{b}^{2}}{{\sin }^{2}}\alpha )}=1\]  \[\Rightarrow \]   \[{{P}^{2}}={{a}^{2}}{{\cos }^{2}}\alpha +{{b}^{2}}{{\sin }^{2}}\alpha \]

Hence proved.