-
If A is an invertible matrix of order \[3\times 3\] such that | A| = 5, find the value of \[|{{A}^{-1}}|.\]
View Answer play_arrow
-
If A, B and C are the vertices of \[\Delta ABC,\]what is the value of \[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}?\]
View Answer play_arrow
-
The sides of an equilateral triangle are increasing at the rate of 2 cm/s. Find the rate at which the area increases, when the side is 10 cm.
View Answer play_arrow
-
Evaluate \[\int{\frac{1}{x{{(\log \,x)}^{n}}}\,dx.}\]
View Answer play_arrow
-
Find the integrating factor of differential equation \[\frac{dy}{dx}+y\tan x-\sec x=0.\]
View Answer play_arrow
-
Find the projection of vector \[2\hat{i}+\hat{j}\] on the vector \[\hat{i}+2\hat{j}.\]
View Answer play_arrow
-
Let A and B be square matrices of the order \[3\times 3.\]Is \[{{(AB)}^{2}}={{A}^{2}}{{B}^{2}}?\] Give reason.
View Answer play_arrow
-
If \[{{x}^{16}}{{y}^{9}}={{({{x}^{2}}+y)}^{17}},\] then prove that \[x\frac{dy}{dx}=2y.\]
View Answer play_arrow
-
Find the value of m and n, where m and n are order and degree of differential equation \[\frac{4{{\left( \frac{{{d}^{2}}y}{d{{x}^{2}}} \right)}^{3}}}{\frac{{{d}^{3}}y}{d{{x}^{3}}}}+\frac{{{d}^{3}}y}{d{{x}^{3}}}={{x}^{2}}-1.\]
View Answer play_arrow
-
Find the approximate value of \[\frac{1}{\sqrt{251}}.\]
View Answer play_arrow
-
If the slope of the curve \[2{{y}^{2}}=a{{x}^{2}}+b\] at \[(1,\,\,-\,1)\] is \[-\,1,\] find the values of a and b.
View Answer play_arrow
-
There are 5 white and 8 red balls in bag A, 7 white and 6 red balls in bag B, 6 white and 5 red balls in bag C. One ball is taken out at random from each bag. Find the probability that all the three balls are of the same colour.
View Answer play_arrow
-
A total amount of Rs. 7000 is deposited in three different saving bank accounts with annual interest rates of 5%, 8% and \[8\frac{1}{2}%,\] respectively. The total annual interest from these three accounts is Rs. 550. Equal amounts have been deposited in the 5% and 8% saving accounts. Find the amount deposited in each of the three accounts, with the help of matrix multiplication. Keeping nation's growth in mind, justify the value of saving in individual life.
View Answer play_arrow
-
Find the intervals in which \[f(x)=\frac{3}{10}{{x}^{4}}-\frac{4}{5}{{x}^{3}}-3{{x}^{2}}+\frac{36}{5}x+11\] is (a) Strictly increasing (b) strictiy decreasing.
View Answer play_arrow
-
Differentiate \[{{\tan }^{-1}}\left( \frac{a\cos x-b\sin x}{b\cos x+a\sin x} \right),\] \[\frac{-\,\pi }{2}<x<\frac{\pi }{2}\] and \[\frac{a}{b}\tan x>-\,1\,\,w.r.t.x.\]
View Answer play_arrow
-
\[\] Prove that \[{{\cot }^{-1}}7+{{\cot }^{-1}}8+{{\cot }^{-1}}18={{\cot }^{-1}}3.\]
View Answer play_arrow
-
Evaluate \[\int{{{x}^{2x}}(1+\log \,x)dx.}\]
View Answer play_arrow
-
| Evaluate \[\int_{0}^{\pi /2}{\log (\sin \,x)\,dx.}\] |
| OR |
| Evaluate \[\int{\frac{{{\sin }^{6}}x+{{\cos }^{6}}x}{{{\sin }^{2}}{{\cos }^{2}}x}}\,dx.\] |
View Answer play_arrow
-
Find a unit vector perpendicular to each of the vectors \[\vec{a}+\vec{b}\] and \[\vec{a}-\vec{b},\] where \[\vec{a}=3\hat{i}+2\hat{j}+2\hat{k}\] and \[\vec{b}=\hat{i}+2\hat{j}-2\hat{k}.\]
View Answer play_arrow
-
Find the foot of perpendicular drawn from the point A (1, 8, 4) to the line joining the points \[B(0,\,\,-\,1,\,\,3)\] and \[C(2,\,\,-3,\,\,1).\]
View Answer play_arrow
-
| For 6 trials of an experiment, let X be a binomial variate which satisfies the relation 9P(X = 4) = P(X = 2). Find the probability of success. |
| OR |
| A bag A contains 4 black and 6 red balls and bag B contains 7 black and 3 balls. A die is thrown. If 1 or 2 appears on it, then bag A is chosen, otherwise bag B. If two balls are drawn at random (without replacement) from the selected bag, find the probability of one of them being red and another black. |
View Answer play_arrow
-
Two groups are competing for the position on the board of directors of a corporation. The probability that the first and second groups will win are 0.6 and 0.4, respectively. Further, if the first group wins the probability of introducing a new product is 0.7 and the corresponding probability is 0.3, if the second group wins. Find the probability that the new product introduce was by the second group.
View Answer play_arrow
-
| Show that the differential equation \[\left[ x\,{{\sin }^{2}}\left( \frac{y}{x} \right)-y \right]\,dx+x\,dy=0\] |
| Is homogeneous. Find the particular solution of this differential equation, given that \[y=\frac{\pi }{4},\] when x = 1. |
| OR |
| Find the solution of differential equation |
| \[{{x}^{2}}dy+y(x+y)dx=0,\] if x = 1 and y = 1. |
View Answer play_arrow
-
| Consider the function \[f:{{R}^{+}}\to [4,\,\,\infty )\] defined by \[f(x)={{x}^{2}}+4,\] where \[{{R}^{+}}\] is the set of all non-negative real numbers. Show that f is invertible. Also, find the inverse of f. |
| OR |
| Show that the relation S in the set |
| \[A=\{x\in Z:0\,\,\le x\le 12\}\] given by |
| \[S=\{(a,\,\,b):a,\,\,b\in Z,\,\,|a-b|\]is divisible by 4} is an equivalence relation. Find the set of all elements related to 4. |
View Answer play_arrow
-
Show that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View Answer play_arrow
-
Find the area of region bounded by lines \[y=\frac{5}{2}x-5,\] \[x+y-9=0\] and \[y=\frac{3}{4}x-\frac{3}{2}.\]
View Answer play_arrow
-
| Find the equation of plane determined |
| by points \[A(3,\,\,-\,1,\,\,2),\] B(5, 2, 4), \[C(-\,1,\,\,-\,1,\,\,6)\] and hence find the distance between plane and point P(6, 5, 9). |
| OR |
| Show that the lines |
| \[\vec{r}=3\hat{i}+2\hat{j}-4\hat{k}+\lambda (\hat{i}+2\hat{j}+2\hat{k})\] and |
| \[\vec{r}=5\hat{i}-2\hat{j}+\mu (3\hat{i}+2\hat{j}+6\hat{k})\] are intersecting. |
| Hence, find their point of intersection. |
View Answer play_arrow
-
A cooperative society of farmers has 50 hec of land to grow two crops A and B. The profit from crops A and B per hectare are estimated as Rs.10500 and Rs. 9000, respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 L/hec and 10 L/hec, respectively. Further not more than 800 L, herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land keeping in mind that the protection of fish and other wildlife is more important than earning profit. How much land should be allocated to each crop, so as to maximise the total profit formulate the above as an LPP and solve it graphically. Do you agree with the message that the protection of wild life is at most necessary to preserve the balance in environment
View Answer play_arrow
-
If 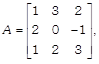 then show that A satisfies the following equation. then show that A satisfies the following equation. |
| \[{{A}^{3}}-4{{A}^{2}}+11I-3A=O\] |
| OR |
| If \[A+B+C=\pi ,\]show that |
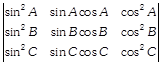 |
| \[=-\sin (A\,-B)sin(B\,-C)sin(C\,-A).\] |
View Answer play_arrow
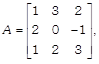 then show that A satisfies the following equation.
then show that A satisfies the following equation.