question_answer

Show that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.

Answer:

Let ABC be a triangle inscribed in a given circle with centre O and radius r. The area of the triangle will be maximum if its vertex A opposite to the base BC is at a maximum distance from the base BC. This is possible only when A lies on the diameter perpendicular to BC. Thus, \[AD\bot BC.\] So, \[\Delta \,ABC\]must be an isoscele triangle. Let\[OD=x.\] 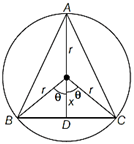Applying Pythagoras theorem in right angled \[\Delta \,ODB\]we get \[O{{B}^{2}}=O{{D}^{2}}+B{{D}^{2}}\] \[\Rightarrow \]   \[{{r}^{2}}={{x}^{2}}+B{{D}^{2}}\] \[\Rightarrow \]   \[BD=\sqrt{{{r}^{2}}-{{x}^{2}}}\] \[\therefore \]                  \[BC=2\,\,BD=2\sqrt{{{r}^{2}}-{{x}^{2}}}\] Also, \[AD=AO+OD=r+x\]. Let A denote the area of\[\Delta \,ABC\]. Then,    \[A=\frac{1}{2}(BC\,\,\times AD)\] \[\Rightarrow \]   \[A=\frac{1}{2}\times 2\sqrt{{{r}^{2}}-{{x}^{2}}}\times (r+x)\] \[\Rightarrow \]   \[A=(r+x)\sqrt{{{r}^{2}}-{{x}^{2}}}\] \[\Rightarrow \]   \[\frac{dA}{dx}=\sqrt{{{r}^{2}}-{{x}^{2}}}-\frac{x\,(r+x)}{\sqrt{{{r}^{2}}-{{x}^{2}}}}\] [differentiating w.r.t. x] \[\Rightarrow \]   \[\frac{dA}{dx}=\frac{{{r}^{2}}-rx-2{{x}^{2}}}{\sqrt{{{r}^{2}}-{{x}^{2}}}}\] The critical numbers of A are given by\[\frac{dA}{dx}=0\] \[\therefore \]                  \[\frac{dA}{dx}=0\Rightarrow \frac{{{r}^{2}}-rx-2{{x}^{2}}}{\sqrt{{{r}^{2}}-{{x}^{2}}}}=0\] \[\Rightarrow \]   \[(r-2x)\,\,(r+x)=0\] \[\Rightarrow \]   \[r-2x=0\Rightarrow x=\frac{r}{2}\] Now,     \[\frac{dA}{dx}=\frac{{{r}^{2}}-rx-2{{x}^{2}}}{\sqrt{{{r}^{2}}-{{x}^{2}}}}\] \[\Rightarrow \]   \[\frac{{{d}^{2}}A}{d{{x}^{2}}}=\frac{(-r-4x)}{\sqrt{{{r}^{2}}-{{x}^{2}}}}+\frac{({{r}^{2}}-rx-2{{x}^{2}})x}{{{({{r}^{2}}-{{x}^{2}})}^{3/2}}}\] [differentiating both sides w.r.t. x] \[\Rightarrow \]   \[{{\left( \frac{{{d}^{2}}A}{d{{x}^{2}}} \right)}_{x=\frac{r}{2}}}=-\,2\sqrt{3}<0\] Thus, A is maximum when\[x=\frac{r}{2}\]. \[\therefore \]                  \[BD=\sqrt{{{r}^{2}}-{{x}^{2}}}\] \[\Rightarrow \]   \[BD=\frac{\sqrt{3}r}{2}\] In right angled\[\Delta \,ODB\], \[\tan \theta =\frac{BD}{OD}\Rightarrow \tan \theta =\frac{\frac{\sqrt{3}r}{2}}{\frac{r}{2}}=\sqrt{3}\Rightarrow \theta =60{}^\circ \] \[\therefore \]      \[\angle BAC=\theta =60{}^\circ \] But\[AB=AC.\]Therefore, \[\angle B=\angle C=60{}^\circ .\] Thus, we obtain \[\angle A=\angle B=\angle C=60{}^\circ .\] Hence, A is maximum when ABC is an equilateral triangle. Hence proved.