-
Find matrix X, if
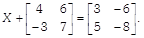
-
Evaluate \[\int_{0}^{\pi /2}{x\,\sin \,x\,dx.}\]
View Answer play_arrow
-
Find the value of \[\frac{dy}{dx},\] if \[y=\cos ({{\sec }^{-1}}x+\text{cose}{{\text{c}}^{-1}}x),\] \[|x|\,\,\ge 1.\]
View Answer play_arrow
-
Find the volume of a parallelopiped whose sides are given by \[-\,3\hat{i}+7\hat{j}+5\hat{k},\] \[-\,5\hat{i}+7\hat{j}-3\hat{k}\] and \[7\hat{i}-5\hat{j}-3\hat{k}.\]
View Answer play_arrow
-
Examine the continuity of the function \[f(x)=\left\{ \begin{matrix} \frac{|\sin \,x|}{x} & x\ne 0 \\ 1, & x=0\,\,\text{at}\,\,x=0 \\ \end{matrix} \right.\]
View Answer play_arrow
-
Evaluate
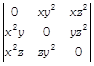
-
Solve the following differential equation. \[\frac{dy}{dx}=1-x+y-xy\]
View Answer play_arrow
-
Show that the function given by f(x) = sinx is neither strictly decreasing nor strictly increasing in the interval \[(0,\,\,\pi ).\]
View Answer play_arrow
-
Find \[\frac{dy}{dx},\] if \[y={{\sin }^{-1}}\left( \frac{1-{{x}^{2}}}{1+{{x}^{2}}} \right),\] \[0<x<1.\]
View Answer play_arrow
-
A speak truth in 30% of the case and B is 60% of the case. In what percentage of cases are likely to contradict each other in stating the same fact?
View Answer play_arrow
-
If \[\vec{a}\] and \[\vec{b}\] are two vectors, then show that \[{{(\vec{a}\times \vec{b})}^{2}}+{{(\vec{a}\cdot \vec{b})}^{2}}={{a}^{2}}{{b}^{2}}.\]
View Answer play_arrow
-
Find the value of \[\int_{-\pi /4}^{\pi /4}{({{x}^{3}}+{{x}^{4}}+{{\tan }^{3}}x)\,dx.}\]
View Answer play_arrow
-
| Use matrix product |
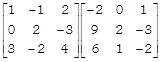 to solve the system of equations to solve the system of equations |
| \[x-y+2z=1,\] \[2y-3z=1\] |
| and \[3x-2y+4z=2.\] |
| OR |
| The sum of three numbers is 6. Twice the third number when added to the first number gives 7. On adding the sum of the second and third numbers to thrice the first number, we get 12. Find the numbers, using matrix method. |
View Answer play_arrow
-
Find the value of \[\sin \left\{ 2{{\cot }^{-1}}\left( -\frac{5}{12} \right) \right\}.\]
View Answer play_arrow
-
Evaluate \[\int{\frac{\sqrt{{{x}^{2}}+1}[\log |{{x}^{2}}+1|-\,2\,\log |x|]}{{{x}^{4}}}}dx.\]
View Answer play_arrow
-
An expensive square piece of golden colour board of side 24 cm is to be made into a box of without top by cutting a square from each corner and folding the flaps to form a box. What should be the side of the square piece to be cut from each corner of the board to hold maximum volume and minimise the wastage? What is the importance of minimising the wastage in utilising the resources?
View Answer play_arrow
-
Evaluate \[\int{\frac{({{x}^{2}}+1)({{x}^{2}}+2)}{({{x}^{2}}+3)({{x}^{2}}+4)}dx.}\]
View Answer play_arrow
-
| Verify Rolle's theorem for the function |
| \[f(x)=\log \left\{ \frac{{{x}^{2}}+ab}{x(a+b)} \right\}\] on [a, b], where 0<a<b. |
| OR |
| Show that the function \[f(x)=\,\,|x+1|+|x-1|,,\] \[\forall \,x\in R\] is not differentiable at the points \[x=-\,1\] and x = 1. |
View Answer play_arrow
-
Find the equation of the plane passing through the points \[(-\,1,\,\,2,\,\,0),\] \[(2,\,\,2,\,\,-\,1),\] and parallel to the line \[\frac{x-1}{1}=\frac{2y+1}{2}=\frac{z+1}{-\,1}.\]
View Answer play_arrow
-
| Solve the differential equation |
| \[y{{e}^{y}}dx=({{y}^{3}}+2x{{e}^{y}})\,dy,\] y(0) = 1 |
| OR |
| Find the differential equation of the family of curves \[y={{e}^{2x}}(acos2x+b\sin 2x),\] where a and b are arbitrary constants. |
View Answer play_arrow
-
A football match may be either won, drawn or lost by the host country's team. So, there are three ways of forecasting the result of any one match i.e. one correct and two incorrect. Find the probability of forecasting atleast three correct results for four matches.
View Answer play_arrow
-
Simplify \[[\begin{matrix} \vec{a}-b & \vec{b}-\vec{c} & \vec{c}-\vec{a} \\ \end{matrix}].\]
View Answer play_arrow
-
An urn contains m white and n black balls. A ball is drawn at random and is put back into the urn along with k additional balls of the same colour as that of the ball drawn. A ball is again drawn at random. Show that the probability of drawing a white ball does not depend on k.
View Answer play_arrow
-
| Show that the function f: \[R\to R\] defined by |
| \[f(x)=\frac{3x-1}{2},\] \[x\in R\] is one-one and onto functions. Also, find the inverse of the function f. |
| OR |
| Examine which of the following is a binary operation and check whether the operation is commutative and associative? |
| (i) On \[{{Z}^{+}},\] define \[a*b={{2}^{ab}}.\] |
| (ii) On Q, define \[a*b=\frac{ab}{2}.\] |
View Answer play_arrow
-
Two farmers Hariom and Siyaram cultivates only three varieties of rice namely Basmati, Permal and Naura. The sale (in Rs.) of these varieties of rice by both the farmers in the month of September and October are given by the following matrices A and B. September Sales (in Rs.) Basmati Permal Naura \[\begin{align} & \text{Basmati}\,\,\,\,\,\,\,\text{Parmal}\,\,\,\,\,\,\,\text{Naura} \\ & A=\left[ \begin{matrix} 10000 & 20000 & 30000 \\ 50000 & 30000 & 10000 \\ \end{matrix} \right]\begin{matrix} \text{Hariom} \\ \text{siyaram} \\ \end{matrix} \\ \end{align}\] October Sales (in Rs.) \[\begin{align} & \text{Basmati}\,\,\,\,\,\,\,\text{Parmal}\,\,\,\,\,\,\,\text{Naura} \\ & B=\left[ \begin{matrix} 5000 & 10000 & 6000 \\ 20000 & 10000 & 10000 \\ \end{matrix} \right]\begin{matrix} \text{Hariom} \\ \text{siyaram} \\ \end{matrix} \\ \end{align}\] (i) Find the combined sales in September and October for each farmer in each variety. (ii) Find the decrease in sales from September to October. (iii) If both farmers receive 2% profit on gross sales, then compute the profit for each farmer and for each variety sold in October. Which variety of rice preferred the most and why?
View Answer play_arrow
-
| Draw a rough sketch of \[{{y}^{2}}=x+1\] and \[{{y}^{2}}=-\,x+1\] and determine the area enclosed by the two curves. |
| OR |
| Draw a rough sketch of \[y=\sin 2x\] and determine the area enclosed by the two curves, X-axis and lines \[x=\frac{\pi }{4}\] and \[\frac{3\pi }{4}.\] |
View Answer play_arrow
-
Find the angle of intersection of the curves \[{{y}^{2}}=4ax\] and \[{{x}^{2}}=4by.\]
View Answer play_arrow
-
| From the point P (1, 2, 4), a perpendicular is drawn on the plane \[2x+y-2z+3=0.\] |
| Find the equation, the length and the coordinates of the foot of the perpendicular. |
| OR |
| Show that the lines |
| \[\vec{r}=(-\,3\hat{i}+\hat{j}+5\hat{k})+\lambda (-\,3\hat{i}+\hat{j}+5\hat{k})\] and |
| \[\vec{r}=(-\,\hat{i}+2\hat{j}+5\hat{k})+\mu (-\,\hat{i}+2\hat{j}+5\hat{k})\] |
| are coplanar. Also, find the equation of the plane containing these lines. |
View Answer play_arrow
-
There are two factories located at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are 8 and 6 units respectively. The cost of transportation per unit is given below
| To From | Cost (in Rs.) |
| A | B | C |
| P | 160 | 100 | 150 |
| Q | 100 | 120 | 100 |
How many units should be transported from each factory to each depot in order that the transportation cost is minimum? What is the minimum transportation cost?
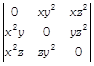
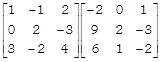 to solve the system of equations
to solve the system of equations 