question_answer

Draw a rough sketch of \[{{y}^{2}}=x+1\] and \[{{y}^{2}}=-\,x+1\] and determine the area enclosed by the two curves.

OR

Draw a rough sketch of \[y=\sin 2x\] and determine the area enclosed by the two curves, X-axis and lines \[x=\frac{\pi }{4}\] and \[\frac{3\pi }{4}.\]

Answer:

Given curves are \[{{y}^{2}}=x+1\]                  ...(i)

and       \[{{y}^{2}}=-\,x+1\]                           ?(ii)

On solving Eqs. (i) and (ii), we get

\[x+1=-x+1\]

\[\Rightarrow \]   \[2x=1-1\]

\[\Rightarrow \]   \[2x=0\]

\[\Rightarrow \]   x = 0

On putting x = 0 in Eq. (i), we get

\[{{y}^{2}}=1\]

\[\Rightarrow \]   \[y=\pm \,1\]

\[\therefore \] Two given parabolas intersect each other at and \[B(0,\,\,-\,1)\] as shown in the figure.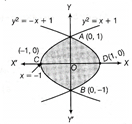

\[\therefore \] Required area = 2 [Area of the region OCAO + Area of the region ODAO]

\[=2\left[ \int_{-\,1}^{0}{\sqrt{x+1}}dx+\int_{0}^{1}{\sqrt{1-x}dx} \right]\]

\[=2\left\{ \left[ \frac{{{(x+1)}^{^{\frac{3}{2}}}}}{\frac{3}{2}} \right]_{-\,1}^{0}+\left[ (-\,1)\frac{{{(1-x)}^{\frac{3}{2}}}}{\frac{3}{2}} \right]_{0}^{1} \right\}\]

\[=2\times \frac{2}{3}\{[{{(x+1)}^{3/2}}]_{-1}^{0}-[{{(1-x)}^{3/2}}]_{0}^{1}\}\]

\[=\frac{4}{3}[\{{{(0+1)}^{3/2}}-{{(-1+1)}^{3/2}}\}-\{{{(1-1)}^{3/2}}-{{(1-0)}^{3/2}}\}]\]\[=\frac{4}{3}[1\,+1]=\frac{8}{3}\text{sq}\,\,\text{units}\]

OR

Given equation of curve is\[y=\sin 2x\]

and the equation of lines are \[x=\frac{\pi }{4}\] and \[x=\frac{3\pi }{4}.\]

To draw the graph of y = sin2x , et us consider the following values of sin2x at various points.

X 0 \[\pi /4\] \[\pi /2\] \[3\pi /4\] \[\pi \] \[5\pi /4\] 2x 0 \[\pi /2\] \[\pi \] \[3\pi /2\] \[2\pi \] \[5\pi /2\] \[\mathbf{y=sin 2x}\] 0 1 0 \[-1\] 0 1

Now, let us draw the graph of y = sin2x as shown below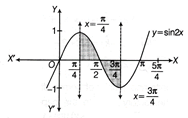

Clearly, the required area is the shaded area, which is given by

\[\int_{\pi /4}^{\pi /2}{y\,dx}+\int_{\pi /2}^{3\pi /4}{(-\,y)}\,dx\]

\[=\int_{\pi /4}^{\pi /2}{(\sin \,2x)dx}+\int_{\pi /2}^{3\pi /4}{(-\,\sin 2x)}\,dx\]

\[=-\frac{1}{2}\left[ \cos 2x \right]_{\pi /4}^{\pi /2}+\frac{1}{2}\left[ \cos 2x \right]_{\pi /2}^{3\pi /4}\]

\[=-\frac{1}{2}\left[ \cos \pi -cos\frac{\pi }{2} \right]+\frac{1}{2}\left[ \cos \frac{3\pi }{2}-\cos \pi  \right]\]\[=-\frac{1}{2}\left[ -\,1-0 \right]+\frac{1}{2}[0-(-\,1)]=\frac{1}{2}+\frac{1}{2}=1\,\,\text{sq}\,\,\text{unit}\]