question_answer

From the point P (1, 2, 4), a perpendicular is drawn on the plane \[2x+y-2z+3=0.\]

Find the equation, the length and the coordinates of the foot of the perpendicular.

OR

Show that the lines

\[\vec{r}=(-\,3\hat{i}+\hat{j}+5\hat{k})+\lambda (-\,3\hat{i}+\hat{j}+5\hat{k})\] and

\[\vec{r}=(-\,\hat{i}+2\hat{j}+5\hat{k})+\mu (-\,\hat{i}+2\hat{j}+5\hat{k})\]

are coplanar. Also, find the equation of the plane containing these lines.

Answer:

Given equation of plane is

\[2x+y-2z+3=0\]                       ?(i)

\[\therefore \] DR's of normal to the plane are 2, 1 and \[-2\]

Also, the given point is (1, 2, 4).

Let M be the foot of perpendicular drawn from P to the plane.

So, DR's of PM is proportional to the DR's of normal to the plane, i.e.  \[2,\,\,1,\,\,-2.\]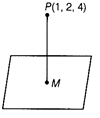

Now, equation of line PM is

\[\frac{x-1}{2}=\frac{y-2}{1}=\frac{z-4}{-\,2}=\lambda \,\,(say)\]

\[\left[ \text{by}\,\,\text{using}\,\,\frac{x-{{x}_{1}}}{a}=\frac{y-{{y}_{1}}}{b}=\frac{z-{{z}_{1}}}{c} \right]\]

Then, coordinates of

\[M=(2\lambda +1,\,\,\lambda +2,\,\,-2\lambda +4)\]                   ?(ii)

Since, the point M lies in the plane (i).

\[\therefore \] \[2(2\lambda +1)+(\lambda +2)-2(-\,2\lambda +4)+3=0\]

\[\Rightarrow \]   \[4\lambda +2+\lambda +2+4\lambda -8+3=0\]

\[\Rightarrow \]   \[9\lambda -1=0\]

\[\Rightarrow \]   \[\lambda =\frac{1}{9}\]

On putting the value of \[\lambda \] in Eq. (ii), we get

Coordinates of \[M=\left( \frac{2}{9}+1,\,\,\frac{1}{9}+2,\,\,\frac{-\,2}{9}+4 \right)\]

\[=\left( \frac{11}{9},\,\,\frac{19}{9},\,\,\frac{34}{9} \right)\]

Now, length of perpendicular PM from point (1, 2, 4) to the plane \[2x+y-2z+3=0\] is

\[PM=\left| \frac{2(1)+2-2(4)+3}{\sqrt{{{(2)}^{2}}+{{(1)}^{2}}+{{(-\,2)}^{2}}}} \right|\]

\[=\left| \frac{2+2-8+3}{\sqrt{4+1+4}} \right|\]

\[=\left| \frac{-\,1}{\sqrt{9}} \right|=\frac{1}{3}\,\,\,\text{unit}\]

Hence, the required equation of line is

\[\frac{x-1}{2}=\frac{y-2}{1}=\frac{z-4}{-\,2}\]

\[\therefore \] Length of perpendicular, \[PM=\frac{1}{3}\] unit and foot of perpendicular, \[M=\left( \frac{11}{9},\,\,\frac{19}{9},\,\,\frac{34}{9} \right)\]

OR

Given equation of lines are

\[\vec{r}=(-\,3\hat{i}+\hat{j}+5\hat{k})+\lambda (-\,3\hat{i}+\hat{j}+5\hat{k})\]

and       \[\vec{r}=(-\hat{i}+2\hat{j}+5\hat{k})+\mu (-\hat{i}+2\hat{j}+5\hat{k})\]

On comparing with \[\vec{r}={{\vec{a}}_{1}}+\lambda {{\vec{b}}_{1}}\] and \[\vec{r}={{\vec{a}}_{2}}+\mu {{\vec{b}}_{2}}\]we get

\[{{\vec{a}}_{1}}=-\,3\hat{i}+\hat{j}+5\hat{k},\] \[{{\vec{b}}_{1}}=-\,3\hat{i}+\hat{j}+5\hat{k}\]

and       \[{{\vec{a}}_{2}}=-\,\hat{i}+2\hat{j}+5\hat{k},\] \[{{\vec{b}}_{2}}=-\,\hat{i}+2\hat{j}+5\hat{k}\]

Now,     \[{{\vec{a}}_{2}}-{{\vec{a}}_{1}}=(-\,\hat{i}+2\hat{j}+5\hat{k})-(-\,3\hat{i}+j+5\hat{k})\]

\[=2\hat{i}+\hat{j}+0\hat{k}\]

Condition for coplanarity of two lines is

\[({{\vec{a}}_{2}}-{{\vec{a}}_{1}})\cdot ({{\vec{b}}_{1}}\times {{\vec{b}}_{2}})=0.\]

\[\therefore \]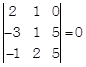

\[\Rightarrow \] \[2(5-10)-1(-15+5)+0=0\] \[\Rightarrow \]

\[-10+10+0=0\]

\[\Rightarrow \]   0 = 0

So, the given lines are coplanar.

Now, the equation of a plane containing two lines is

\[(\vec{r}-{{\vec{a}}_{1}})\cdot ({{\vec{b}}_{1}}\times {{\vec{b}}_{2}})=0.\]

or \[\vec{r}\cdot ({{\vec{b}}_{1}}\times {{\vec{b}}_{2}})={{\vec{a}}_{1}}\cdot ({{\vec{b}}_{1}}\times {{\vec{b}}_{2}})\]

Here,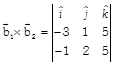

\[=\hat{i}(5-10)-\hat{j}(-15+5)+\hat{k}(-\,6+1)\]

\[=-\,5\hat{i}+10\hat{j}-5\hat{k}=5(-\hat{i}+2\hat{j}-k)\]

\[\therefore \] Required equation of the plane is

\[\vec{r}\cdot 5(-\,i+2\hat{j}-\hat{k})=(-\,3\hat{i}+\hat{j}+5\hat{k})\]

\[\cdot [5(-\,\hat{i}+2\hat{j}-\hat{k})]\]

\[\Rightarrow \]   \[\vec{r}\cdot 5(-i+2\hat{j}-\hat{k})=5(3+2-5)\]

\[\Rightarrow \]   \[\vec{r}\cdot (-i+2\hat{j}-\hat{k})=0\]