9th Class Mental Ability Series Completion

Series Completion

Category : 9th Class

SERIES COMPLETION

Learning Objectives

Introduction
Letter Series
Types of Problems
Number Series
Mixed series

Introduction

In a verbal series, words, letters or digits are given in a specific sequence or order. This section deals with questions in which series of numbers or letters are given. The term follows a certain pattern throughout. Find out the next word, letter or digit to complete the given series. As it is, there is no set pattern and each question may follow a different pattern or sequential arrangement of letters or digits. Which you have to detect using common series and reasoning ability.

There are mainly three types of verbal series completion patterns.

Letter series
Number series

3. Letter and Number mixed series letter

Type -1

Letter Series

This type of question usually consists of a series of small Setters which follow a certain pattern. However some letters are missing from the series. These missing letters are given in a propel sequence as one of the alternatives.

Example:

(i) C D E F G H I

(ii) F E D C B A

(iii) ABC BCD CDE DEF

Note: An element of a series is a single member (identity) of that particular series. For example, in a letter series 'ABCD', each A, B, C and D is a single element. Point to be noted that an element can be made with more than one letter in a series of 'AB LE BE' each AB, LE and B is a single element.

Properties of Letter Series

This is a basic fundamental knowledge of letter series.

A letter series can be in forward order.
A letter series can be in reverse or backward order
A letter series can be in random or jumbled order
A letter series must have more than one element.
Letters can be repeated in a letter series.
A single letter series can have more than one series.

Example:

Direction: in each of the following series determine the order of the letters and select the one from the given options which will complete the given series.

B Y C X D W E ?

(a) S (b) T

(e) None of these

Answer (d)

Explanation: Option (d) is correct. There are two alternate series.

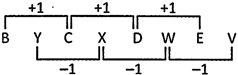
Series I: BCDE (natural order)

Series II: YXWV (reverse order)

A D C G E ?

(a) G (b) J

(w) None of these

Answer (b)

Explanation: Option (b) is correct. There are two alternate series.

Series I: ACE (follows + 2 pattern)

Series II: DGJ (follows + 3 pattern)

L N P R T ?

(a) U (b) V

(e) None of these

Answer (b)

Explanation: Option (b) is correct. The series follows the+2 pattern, i.e.

X O I F ?

(a) D (b) F

(e) None of these

Answer (b)

Explanation: Option (b) is correct. The series follows the sequence of the difference decreasing by 3 i.e.

D Q G O J M ?

(a) K (b) P

(e) None of these

Answers (c)

Explanation: Option (c) is correct. There are two alternate series.

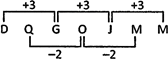
Series I: DGJM (follows + 3 pattern)

Series II: QOM (follows – 2 pattern)

B A F E J I P O ? U

(a) V (b) T

(e) None of these

Answer: (a)

Explanation: Option (a) is correct. Each vowel (AEIOU) is preceded by the letter that comes next to it in the natural alphabetical series.

Z A AY B B X C ?

(a) W (b) C

(e) None of these

Answer: (b)

Explanation: Option (b) is correct. There are three alternate series. The second and the third set are the same, i.e.,

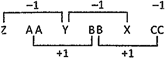
Series I: ZYX (In reverse order)

Series II and III: ABC (in natural order). The letter ‘C’ needs to be repeated.

B D G K ? V

(a) N (b) P

(e) None of these

Answer: (b)

Explanation: Option (b) is correct. The difference between the letters increases at each step after beginning with two.

V R O K ? D

(a) L (b) I

(e) None of these

Answer (c)

Explanation: Option (c) is correct. The letters are in reverse series and the difference four and three alternately.

(a) Q (b) S

(e) None of these

Answer (c)

Explanation: Option (c) is correct. The letters in this series are moved two steps backward.

Types of Problems

(a) Problems based on increasing order series

(b) Problems based on decreasing order series

Problems Based on Increasing Order Series

In such series, letters coming later in the English alphabet placed after the letters coming earlier in the English alphabet. Such series is also known as forward order series.

Example:

In the following questions, various terms of letter series are given with one term missing. Choose the missing term out of the given alternatives.

J L N P R T ?

(a) S (b) U

(e) None of these

Answer: (c)

Explanation: Option (c) is correct. This series is formed by skipping on letter each time.

F I M P ?

(a) V (b) Q

(e) None of these

Answer: (c)

Explanation: Option (c) is correct. This series is formed by following order

Problems Based on Decreasing Order Series

In such series, letters coming later in the English alphabet placed before the letters coming earlier in the English alphabet. This series is also called reverse order backward order series.

Example

U R O L I.........

Series pattern:

Clearly, every next letter takes place 3 letters backward.

Example

H F D B ....

Series pattern: Every next letter takes place skipping one letter in reverse order.

Problems Based on a Series having Mixed Series

In this type of questions, a series of single, pairs or groups of letters or combinations of letter and numerals is given. The terms of the series form a certain pattern as regards the position of the letters in the English alphabet. The candidate is required to decipher this pattern and accordingly find the missing term or the wrong term in the given series.

Example:

Which term comes next in the sequence given below?

AC, FH, KM, PR,?

(a) UW (b) VW

(e) None of these

Answer (a)

Explanation: Option (a) is correct.

Clearly, the first and second letters of each term are moved five steps forward to obtain the corresponding letters of the next term. Thus, the first letter of the missing term must be five steps ahead of P i.e. U, while the second letter must be five steps ahead of R i.e. W. So, the missing term is UW. Hence, the answer is (A).

Find the next term in the series:

BMO, EOQ, HQS, ?

(a) KSU (b) LMN

(e) None of these

Answer (a)

Explanation: Option (A) is correct.

Clearly, we observe the following pattern:

The first letters follow the pattern + 3i.e.

The second letters follow the pattern + 2i.e.

The third letters follow the pattern + 2 i.e.

Thus, the missing term is KSU. Hence, the answer is (A).

Which term comes next in the following series?

YEB, WFD, UHG, SKI, ?

(a) QOL (b) QGL

(e) None of these

Answer (a)

Explanation: Option (A) is correct.

Clearly, we observe the following pattern in the first, second and third letters of the given series:

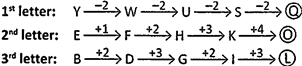
Thus, the missing term is QOL. Hence, the answer is (A).

Which term will replace the question mark in the following series?

ABD, DGK, HMS, MTB, SBL,?

(a) QOL (b) QGL

(e) None of these

Answer: (b)

Explanation: Option (b) is correct.

Clearly, the individual letters of the terms of the given series follow the pattern shown below:

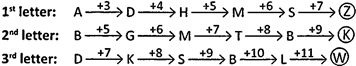
Cyclic Order Series

This type of question usually consists of a series of small letters which follow a certain pattern. However some letters are missing from the series, these missing letters are then given in a proper sequence as one of the alternatives. The candidate is required to choose this alternative as the answer

Example

aab - aaa - bba --

(1) bba (2) abb

(3) bab (4) aab

(5) bbb

The first blank space should be filled in by 'b' so that we have two a's followed by two bs.
The second blank space should be filed in either by 'a'. So that we have four as followed by two bs or by 'b'. So that we have three as followed by three bs.
The last space must be filled in by 'a'.
Thus we have two possible answers- 'baa' and 'bba'. But only 'baa' appears in the alternatives. So the answer is (1).
In case we had both the possible answers in the alternatives, we should choose the one that forms a more prominent pattern/ which is aabb/aaabbb/aa and our answer would have been 'bba'.

Commonly Asked Questions

Directions: In each of the following letter series, some of the letters are missing which are given in that order as one of the alternatives below it. Choose the correct alternative.

ba-ba - bac - acb - cbac

(a) aacb (b) bbca

(e) None of these

Answer: (c)

Explanation: Option (c) is correct.

The series is bac/bac/bac/bac/bac/bac. Thus the pattern bac is repeated.

adb - ac - da - cddcb - dbc" cbda

(a) bccba (b) cbbaa

(e) None of these

Answer: (b)

Explanation: Option (b) is correct.

The series is\[\operatorname{adb}\underline{c}ac\underline{b}da\underline{b}cddcb\underline{a}dbc\underline{a}cbda\]. Here the letters equidistant from the beginning and the end of the series are the same.

a - ba - cbaac - aa - ba

(a) ccbb (b) cabc

(e) None of these

Answer: (b)

Explanation: Option (b) is correct.

The series is acba/acba/acba/acba. Thus, the pattern acba is repeated.

- be - - bb - aabc

(a) acac (b) babe

(e) None of these

Answer (a)

Explanation: Option (a) is correct. The series is abc/cab/bca/abc. Thus, the letters are in cyclic order.

b - b - bb - - bbb - bb - b

(a) bbbbba (b) bbaaab

(e) None of these

Answer (c)

Explanation: Option (c) is correct. The series is babb/bbab/bbba/bbbb. Thus, in each sequence, 'a' moves one step forward and 'b' takes its place and finally in the fourth sequence, it is eliminated.

Type-2

Number Series

Introduction

In this type of series, instead of letters, numbers or digits are used. Number series is divided into 4 types as given below:

(i) Skipping the numbers in same set order

(ii) Addition, subtraction, multiplication or division of numbers to set the next Number in the series.

(iii) Logical transport of numbers.

(iv) Increase/decrease in numbers in a specific order

Example

Which number would replace the question mark (?) in the \[2,\text{ }7,\text{ }14,\text{ }23,\text{ }?,\text{ }47\]

(a) 28 (b) 34

(e) None of these

Answer: (b)

Explanation: Option (b) is correct.

The given sequence is \[+\text{ }5,+\,7,+\,9,\text{ }\_\_\_\_\text{ }ie.\text{ }2+\,\,5\text{ = }7,\text{ }7+7=\text{ }14,\,\,14\text{ }+\text{ }9=23\]

Missing number \[=\text{ }23+11\text{ }=\text{ }34\].

Which is the number that should come next in the following series?

\[4,\text{ }6,\text{ }12,\text{ }14,\text{ }28,\text{ }30,\text{ }\_\_\_\_\_.\]

(a) 32 (b) 64

(e) None of these

Answer: (d)

Explanation: Option (d) is correct.

The given sequence is a combination of two series \[4,\text{ }12,\text{ }28,\text{ }...\] and \[6,\text{ }14,\text{ }30,\text{ }\ldots \]

Clearly the number to be found belongs to the first series. Now the pattern followed is \[+\text{ }8,+16,+\,32\]. So, missing number\[~=\text{ }\left( 28+32 \right)=\text{ }60\]. Hence the answer is (D).

Find the wrong number in the series.

\[7,\text{ }28,\text{ }63,\text{ }124,\text{ }215,\text{ }342\]

(a) 7 (b) 28

(e) None of these

Answer: (b)

Explanation: Option (b) is correct.

The correct sequence is \[{{2}^{3}}-1,\text{ }{{3}^{3}}-1,\text{ }{{4}^{3}}-1,\] ... etc. Here 28 is wrong; so the answer is (B).

Commonly Asked Questions

Directions: In each of the following questions, a number series is given with one term missing.

Choose the correct alternative that will continue the same pattern and replace the question mark in the given series.

\[1,\text{ }9,\text{ }25,\text{ }49,\text{ }?,\text{ }121\]

(a) 64 (b) 81

(e) None of these

Answer: (b)

Explanation: Option (b) is correct. The given series consists of squares of consecutive odd numbers i.e.

\[{{1}^{2}},\,\,{{3}^{2}},\text{ }{{5}^{2}},\,{{7}^{2}}\], ..... So, missing term \[~=\text{ }{{9}^{2}}=81\].

\[2,\text{ }4,\text{ }7,\text{ }12,\text{ }19,\text{ }28,\text{ }?\]

(a) 30 (b) 36

(e) None of these

Answer: (c)

Explanation: Option (c) is correct. The pattern is \[+\,\,3,\,+5,+\,\,1,\,\,+\,\,9,\text{ }.....\]

So, missing term\[=\text{ }28\,\,+11\,\,=\,\,39\].

\[11,\text{ }13,\text{ }17,\text{ }19,\text{ }28,\text{ }23,\text{ }25,\text{ }?\]

(a) 26 (b) 27

(e) None of these

Answer: (c)

Explanation: Option (c) is correct. The pattern is \[+\,2,+\text{ }4,\,+\text{ }2,\,\,+\,\,4,\text{ }.....\]

So, missing term\[=\text{ }25+4=29\].

\[6,\text{ }12,\text{ }21,\text{ }?,\text{ }48\]

(a) 33 (b) 38

(E) None of these

Answer: (a)

Explanation: Option (a) is correct. The pattern is \[+\text{ }6,+9,+12,+15,\text{ }.....\]

So, missing term\[=21+12=33\].

\[2,\text{ }5,\text{ }9,\text{ }?,\text{ }20,\text{ }27\]

(a) 14 (b) 16

(e) None of these

Answer: (a)

Explanation: Option (a) is correct. The pattern is \[+\text{ }3,+\,\,4,+\text{ }5,+\text{ }6,\text{ }.....\]

So sing term \[=\text{ }9\text{ }+\text{ }5=14\]

\[22,\text{ }24,\text{ }28,\text{ }?,\text{ }52,\text{ }84\]

(a) 36 (b) 38

(e) None of these

Answer: (a)

Explanation: Option (a) is correct. The pattern is \[+\text{ }2,+\,4,+\text{ }8+16,\text{ }\ldots \]

So, missing term\[=\text{ }28\,\,+\,\,8=\text{ }36\].

\[10,\text{ }100,\text{ }200,\text{ }310,\text{ }?\]

(a) 400 (b) 410

(e) None of these

Answer (d)

Explanation: Option (d) is correct. The pattern is \[+\text{ }90+100,+110,\text{ }.\ldots \]

So, missing term\[=\text{ }310+120=430\].

\[4,\text{ }9,\text{ }25,\text{ }?,\text{ }121,\text{ }169,\text{ }289,\text{ }361\]

(a) 49 (b) 64

(e) None of these

Answer (a)

Explanation: Option (a) is correct. The given series consists of squares of consecutive prime numbers i.e.\[{{2}^{2}},\,\,{{3}^{2}},\,{{5}^{2}},\text{ }......,\,{{11}^{2}},\text{ }{{13}^{2}},\text{ }{{17}^{2}},\,\,{{19}^{2}}\]. So, missing term \[={{7}^{2}}=49\].

\[1,\text{ }1,\text{ }2,\text{ }6,\text{ }24,\text{ }?,\text{ }720\]

(a) 100 (b) 104

(e) None of these

Answer (d)

Explanation: Option (d) is correct. The pattern is \[\times 1,\,\times \,2,\,\times 3,\,\times 4,\text{ }.....\]

So, missing term \[=\text{ }24\times 5=120\].

\[5760,\text{ }960,\text{ }?,\text{ }48,\text{ }16,\text{ }8\]

(a) 120 (b) 160

(e) None of these

Answer: (c)

Explanation: Option (c) is correct. The pattern is\[\div \,\,6,\,\,\div \,\,5,\,\,\div \,\,4,\,\div 3,\,\,\div \,\,2\] .

So, missing term\[=\,\,960\div \,\,5=192\].

\[2,\text{ }7,\text{ }27,\text{ }107,\text{ }427,\text{ }?\]

(a) 1262 (b) 1707

(e) None of these

Answer (b)

Explanation: Option (b) is correct. The pattern is \[+\text{ }5,+\text{ }20,\,\,+\,\,80,\,+\,\,320,\text{ }...\] \[i.e.+\left( 5\times 12 \right),+\,\,\left( 5\times \,\,22 \right),+\left( 5\times 42 \right),\]

,.....

So, missing term \[=\text{ }427+\,\,\left( 5\times \,\,162 \right)=\text{ }427+1280=1707\]

\[5,\,\,5,\text{ }2,\text{ }7,\text{ }9,\,\,16,\,\,25,\,\,?\]

(a) 41 (b) 45

(e) None of these

Answer (a)

Explanation: Option (a) is correct. Each term in the series, except the first two terms, is the sum of the preceding two terms.

So, missing term\[=\text{ }16+25=41\].

Mathematical Concept of Progressions

Arithmetic Progression (A.P)

In this series patterns are given as below:

a, a + d, a + 2d, a + 3d, a + 4d, ........is known as an A.P.

In case a is first number of series and d is the difference of first (sequentially) two numbers.

Formula of nth term = a + (n ? 1) d

If \[4,\text{ }9,\text{ }14,\text{ }19,\text{ }....\] is an A.P., then find the value of 15th term.

(a) 75 (b) 85

(e) None of these

Answer (c)

Explanation: Option (c) is correct.

First number \[\left( a \right)\text{ }=\text{ }4\]

Difference \[(d)=9-4=5\]

\[(d)=14-9=5\]

\[(d)=19-14=5\].

15th term means number of term is 15.

Here \[a=4,\,d=5,n=15,\] nth term \[=\text{ }a\,\text{+}\,\,\left( n-\text{1} \right)d\]

\[\therefore \,\,{{T}_{15}}=4+(15-1)\,5=\,\,4+14\,\,\times \,\,5=4+70=74\].

Geometric Progression (G.P)

In this series pattern is given below:

\[a,\,\,ar,\,\,a{{r}^{2}},\text{ }a{{r}^{3}}\],..... is known as a G.P

In this series first number is a and common ratio is r. r is divided initially into two numbers.

\[\begin{array}{*{35}{l}}

Formula of nth term = a{{r}^{(n-1)}} \\

\end{array}\]

If \[1,\text{ }4,\,\,16,\,\,64\],….. is a G.P then what will be the 10th term?

(a) 39 (b) 49

(e) None of these

Answer (b)

Explanation: Option (b) is correct. \[1,\text{ }4,\,\,16,\,\,64\],…. G.P.

Here \[a=1,r=\frac{4}{1}=\frac{16}{4}=\frac{64}{16}=4\] and\[n=10\].

Then \[{{n}^{th}}\] term \[=a{{r}^{(n-1)}}\]

\[10th\text{ }term\text{ }=\left( 1 \right)\,\,\times \,\,{{\left( 4 \right)}^{\left( 10\,-\,1 \right)}}\]

\[=\text{ }1\text{ }\times \text{ }{{4}^{9}}={{4}^{9}}\]

Type - 3

Letter and Number mined series

Introduction

In this type of series, both letters and alphabets as well as numerical digits are used. These series are combined, formed on similar patterns as individual letter and number series also.

Example:

Find the next term in letter-number series:

2B, 4C, 8E, 14H, ?

(a) 20 L (b) 22 L

(e) None of these

Answer (B)

Explanation: Option (B) is correct. The sequence of numbers is

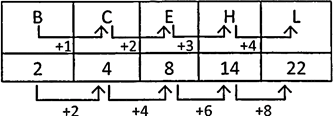
First by number series is \[+\text{ }2,+\,4,+\,6,+\text{ }8,\] and sequence of letters series is \[+\text{ }1,+2,+\,3,\,+\,4\].

Commonly Asked Questions

Directions: In each series given below, what would come in place of the question-mark?

3F, 6G, 11l, 18L?

(a) 27 P (b) 21 O

(e) None of these

Answer: (a)

Explanation: Option (a) is correct. The sequence of numbers is \[+\,3,+\,5,+\,7,+\,9\] and the letters are moved \[1,\text{ }2,\text{ }3,\text{ }4\] steps forward.

51Y, 27S, 9N, 3J?

(a) 0H (b) 1G

(e) None of these

Answer: (b)

Explanation: Option (b) is correct. The numbers are divided by 3 at each step and the letters are moved \[6,\text{ }5,\text{ }4,\text{ }3\] steps backward.

E5, K11, Q17, ?

(a) X20 (b) Y24

(E) None of these

Answer: (d)

Explanation: Option (d) is correct. The series comprises of random letters and numbers indicate the position of the letter in alphabet series.

D2, I3, N6, S18, ?

(a) V72 (b) W36

(e) None of these

Answer: (d)

Explanation: Option (d) is correct. The letters are moved five steps forward and every third number is the product of two preceding numbers.

3J, 6M, 12L, ?, 48N

(a) 24 O (b) 18 M

(e) None of these

Answer (a)

Explanation:

Step 1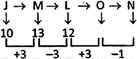

Option (a) is correct. Every number is double the previous number and the sequence of letters is + 3, – 1 (3 steps forward, 1 step backward) which is repeated.

Summary

Note: In a series a set of number is given in such a way that each member or the number satisfies particular definite property. The number of series follow a definite characteristics.

Some of the important properties of these numbers are given below:

Prime number: A counting number greater than 1 which is divisible by itself and 1 only is called a prime number \[2,\text{ }3,\text{ }5,\text{ }7,\text{ }9,\text{ }11,\text{ }13,\text{ }15\] etc.
Odd numbers: A number not divisible by 2 is an odd number eg; \[1,\,\,3,\text{ }5,\text{ }7,\text{ }9,\text{ }11,\text{ }13\] etc.
Even numbers: A number divisible by 2 is an even number e.g; \[2,\text{ }4,\text{ }6,\text{ }8\]etc.
Perfect square: A counting number whose square root is a counting number is called perfect square i.e; \[1,\text{ }4,\text{ }9,\text{ }16,\text{ }25,\text{ }36,\text{ }49,\text{ }64\]etc.
Multiple of numbers: A number which is divisible by a given number Y is called the multiple of Y i.e; \[3,\text{ }6,\text{ }9,\text{ }12,\text{ }15\]etc. are all multiple of 3.
Number in A.P.: Some given numbers are said to be in A.P. (Arithmetic progression, if the difference between two consecutive number is same) i.e; \[15,\text{ }13,\text{ }11,\text{ }9,\text{ }7,\text{ }5,\text{ }3,\text{ }1,-\,1,-\,3,-\,5,\]etc.
Number in G.P.: Some given numbers are in G.P. (Geometric progression] if their ratio between two consecutive numbers remains the same) i.e; 4, 16, 64, 256 etc.

9th Class Mental Ability Series Completion

Other Topics

Notes - Series Completion