7th Class Mathematics Mensuration Mensuration (Perimeter & Area)

MENSURATION (Perimeter and Area)

FUNDAMENTALS                                                

•          Perimeter is the distance around a closed figure.
•         Area is the part of plane occupied by the closed figure.

(a) Perimeter of a square \[=4\times \] side.

Elementary question-1: Find perimeter of a square kabaddi field each of whose side is 20 metres

Ans.     Perimeter \[=4\times 20=80\,m\]

(b) Perimeter of a rectangle \[=2\times \] (length + breadth) units.

(c) Area of a square = (side \[\times \] side).

(d) Area of a rectangle = length \[\times \] breadth.

Elementary Question-2: Find perimeter and area of a football field whose length and breadth are 40 metres and 70 metres respectively.

Ans.     Perimeter  \[=2\times (40+70)=220\,m\]

Area \[=40\times 70=2800\text{ }Sq.\text{ }m.\]                                                              

(e) Area of a parallelogram = base \[\times \] height sq. units.

(f) Area of a triangle \[=\frac{1}{2}\] (Area of the parallelogram generated from it)

\[=\frac{1}{2}\times \]base \[\times \] height sq. units

•           Area of a trapezium \[=\frac{1}{2}\,(a+b)\,h\,sq.\] units, where 'a' and 'b' are lengths of parallel sides and 'h' is the height between them.

•          If the length of sides of a triangle are a, b, c and \[s=\frac{a+b+c}{2}=\] half perimeter, then area is given as  \[\Delta \,=\,\sqrt{s\left( s-a \right)\,\left( s-b \right)\,\left( s-c \right)}\]
•           A circle is a closed curve in a plane drawn in such a way that every point on it is at a constant distance (r units) from a fixed point O inside it.

The fixed point, O is called the centre of the circle and the constant distance r is called the radius of the circle. Here, we can introduce the idea of "locus". Circle is locus of points P whose distance form a fixed point '0' is constant. 'O' is called centre and OP is called radius of the circle.

•           Circumference of a Circle: The perimeter of a circle is called its circumference.
•           Circumference \[=2\pi r=\pi d,\] where r = radius and d = diameter.
•           Here\[\pi \](Pi) is a constant, equal to \[3.14\] approximately.
•           Area of a circle: Area of a circle with radius r units is equal to \[\pi {{r}^{2}}\] units.
•           Area of a Ring:

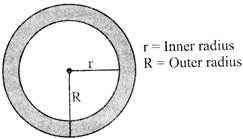
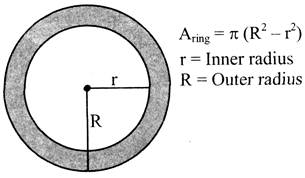
The region enclosed between two concentric circle of different radii is called a ring. Area of path formed between two concentric circular regions \[={{(\pi {{R}^{2}}-\pi r)}^{2}}\,sq.\] sq. units.

\[=\pi ({{R}^{2}}-{{r}^{2}})\] square units

\[=(R+r)\,\,(R-r)\] square units

•          Area of a rhombus \[=\frac{1}{2}{{d}_{1}}\times {{d}_{2}}=\left( \frac{1}{2}\times product\,\,of\,\,diagonals \right)\]