6th Class Mathematics Practical Geometry

 Practical Geometry

• We use the following mathematical instruments to construct geometrical shapes.

(i)   A graduated ruler or scale   

(ii) The compasses     

(iii) The divider  

(iv) Set - squares                

(v) The protractor

• Using a ruler and compasses, we can construct the following:

(i) A circle of a given radius.

(ii) A line segment of a given length.

(iii) A copy of a given line segment.

(iv) A perpendicular to a line through a point

(a) on the line.                (b) not on the line.

(v) The perpendicular bisector of a line segment of given length.

(vi) An angle of a given measure.

(vii) A copy of a given angle.

(viii) The bisector of a given angle.

(ix) Some angles of special measures such as

(a) \[{{90}^{o}}\]                    (b) \[{{45}^{o}}\]      

(c) \[{{60}^{o}}\]                    (d) \[{{30}^{o}}\]     

(e) \[{{120}^{o}}\]                   (f)  \[{{135}^{o}}\]

• A line has no definite length.

• An unlimited number of lines can be drawn, passing through a given point.

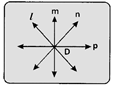
• On a single line, there exist infinite number of points.

Only a single line passes through two distinct points 'A' and 'B'.

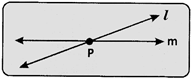
• Intersecting Sines: If there is a point P common to two lines I and m, we say that the two lines intersect at the point P and this point P is called the point of intersection of the given lines.

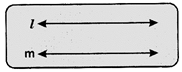
• Parallel lines: The lines which do not intersect each other and do not have any point in common are called parallel lines.

• Concurrent lines: When three or more lines pass through a single point, they are called concurrent lines and the point is called the point of concurrence of the given lines.

• Collinear points: Three or more points in a plane are said to be collinear if they lie on the same line and this line is called the line of collinearity for the given points.

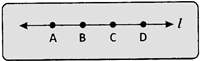
Points that do not lie on the same line are called non-collinear points.

• A circle can be constructed if its radius is known.

• Circles with the same centre but different radii are called concentric circles.

• A perpendicular bisector divides a line segment into two equal parts and meets the segments at right angles.

• The simplest angle that can be constructed with the aid of ruler and compass is that of \[60{}^\circ \].