Number System
Category : 5th Class
Number System
Learning Objectives
Numbers
Numbers are mathematical symbols by which we express date, time, distance, position, quantity etc.
We use ten symbols (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) to write any number.
Like 346562232, 3465452155, 4003444656 etc.
Numbers System
Number system deals with the study of different types of numbers. In this chapter, we will study about the categorization of different types of numbers.
Numbers Types
Numbers are classified according to their type. The first type of numbers we ever learned about: the counting numbers or the natural numbers and the next type of numbers is whole numbers.
Numbers which are not divisible by 2 are called odd numbers. For example, 1, 3, 5, 7, 9, 11, .....etc.
Whole numbers which have at least one factor other than 1 and the number itself are called composite numbers. For example, 4, 6, 8, 9, 12 etc....
For example,....... 5, - 4, - 3, - 2, - 1, 0, + 1, + 2, + 3, + 4, + 5,......
Predecessor of a number is obtained by subtracting 1 from the number. For example. The predecessor of 243 = 243 - 1 = 242.
Hindu-Arabic Numeral System
Hindu-Arabic Numeral System is also known as Indian System of Numeration. This system is based on the following place value chart.
Place Value Chart
|
Period |
Kharabs |
Arabs |
Crores |
Lakhs |
Thousands |
Ones |
|||||||
|
Place |
Ten Kharab (T-KH) 1000000000000 |
Kharab (KH) 100000000000 |
Ten Arab (T-A) 10000000000 |
Arab (a) 10000000000 |
Ten Crores (T-C) 100000000 |
Crores (c) 100000000 |
Ten Lakhs (T-L) 1000000 |
Lakhs (L) 100000 |
Ten Thousands (T-TH) 1000 |
Thousands (TH) 1000 |
Hundred (H) 100 |
Tens (T) 10 |
Ones (O) 0 |
International System of Numeration
International system of numeration is widely used in the most part of the world. The following table shows the place value chart for international System of Numeration:
|
Period |
Billion |
Millions |
Thousands |
Ones |
||||||||
|
Place |
Hundred billions |
Ten billions |
Billions |
Hundred millions |
Ten millions |
Millions |
Hundred thousands |
Ten thousands |
Thousands |
Hundred |
Tens |
Ones |
Points to Remember
For example, 9 + 1 = 10; 99 + 1 - 1000; 999 + 1 - 10000; 9999 + 1 = 100000
Thousand \[\times \] Thousand \[\times \] Thousand \[\times \] Thousand - 1 Trillion, or we can say Thousand Billions make 1 Trillion.
10 Million (10000000) = 1 Crore
1 Billion (1000000000) = 1 Arab
100 Billion (10000000000) = 1 Kharab
1 Trillion (1000000000000) = 10 Kharab
Roman Numeral
Roman numerals represent the numbers using alphabetical symbols.
The seven alphabetical symbols, which are used in Roman system of numeration, and their values are as follows:
|
Symbols I |
Value 1 |
|
V |
5 |
|
X |
10 |
|
L |
50 |
|
C |
100 |
|
D |
500 |
|
M |
1000 |
Rules of Ordering in Mathematics-BODMAS
Brackets: There are three types of brackets:
(i) Small brackets (Parentheses), which is denoted by ( ).
(ii) Middle brackets (Braces), which is denoted by { }.
(iii) Big brackets (Brackets), which is denoted by [ ].
When we use brackets, it is customary to put [ ] outermost, then { } and then
( ) innermost symbols first. For example, \[[\{\left( 4+5 \right)\times ~6\}+7\left] = \right[\{9~\times 6\}+7\left] = \right[54+7]=11\].
BODMAS: When a single expression contains many mathematical operations then BODMAS rules are used for the simplification of the expression. The word BODMAS has been arranged according to the priority of the operations. The BODMAS acronym is for:
Recall that 'of is replaced by multiplication (x). Correct order for numbers in operations is: () {} []\[\div \]\[\times \] or ‘of’ + -
Fractions
Fraction is a number, which is used to represent the part of a whole. It is expressed, in the form of \[\frac{P}{Q}\] where P and Q are natural numbers. The upper part of the fraction is called numerator and the lower part is called denominator. For example, \[\frac{5}{9}\] is a fraction, where 5 is numerator and 9 is denominator.
Commonly Asked Question
(a) 19 (b) 18
(c) 17 (d) 23
(e) None of these
Answer: (c)
Explanation: Predecessor of 19 = 19 - 1 = 18.
18 is not a prime number and just before 18 is 17.
(a) 16, 16, 16, 616
(b) 1, 61, 61, 61, 616
(c) 1, 61, 61, 61, 61, 616
(d) 6, 16, 16, 616
(e) None of these
Answer: (a)
Explanation: Sixteen crore sixteen lakh sixteen thousand six hundred and sixteen
\[=1\times ~100000000+6~\times 10000000+1\times ~1000000+6~\times 100000+1\times ~10000\]
\[+6~\times 1000+6\times ~100+1~\times 10+6~\times 1=161616616=16, 16, 16, 616\].
(a) CMXCVIII (b) CMLXXXIX
(c) CMXXVIII (d) CMLXVIII
(e) None of these
Answer: (a)
Explanation: The greatest three digit even number == 998.
\[=900+90+8=\left( 1000100 \right)+\left( 10010 \right)+8=\text{CM+XC+VIII = CMXCVIII}\].
(a) 56 (b) 52
(c) 53 (d) 58
(e) None of these
Answer: (b)
Explanation: On applying BODMAS, we get,
\[=6+2[3+5\{2812\times ~2\}\left] =6+2 \right[3+5\left\{ 2824 \right\}\left] =6+2 \right[3+5~\times 4]\]
\[=6+2\left[ 3+20 \right]=6+2\times ~23=6+46=52\].
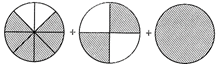
(a) \[2\frac{1}{4}\] (b) \[1\frac{1}{8}\]
(c) \[2\frac{3}{4}\] (d) \[1-\frac{3}{8}\]
(e) None of these
Answer: (a)
Explanation: Here, fraction represented by shaded parts is as follow:
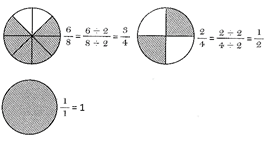
Hence, the required mixed fraction = \[\frac{3}{4}+\frac{1}{2}+1\]
= \[\frac{3\times 1+1\times 2+1\times 4}{4}=\frac{3+2+4}{4}=\frac{9}{4}=2\frac{1}{4}\]
You need to login to perform this action.
You will be redirected in
3 sec
