Fractions
Category : 5th Class
Fractions
Fractions
Faction is a number, which is used to represent the part of a whole. It is expressed, in the form of \[\frac{P}{Q}\] where P and Q are natural numbers. The upper part of the fraction is called numerator and the lower part is denominator. For example, \[\frac{5}{9}\] is a fraction, where 5 is numerator and 9 is denominator.
Represent the shaded part of the figure as a fraction.
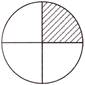
Solution: \[\frac{1}{4}\]
Like Fraction
The fractions, which have the same denominators are called like fractions.
Example:
![]()
Unlike Fraction
The fractions, which do not have the same denominators, in other words, the fractions with different denominators are called unlike fractions.
Unit Fraction
The fractions which have the numerator 1 are called unit fractions.
Proper Fraction
If the numerator of a fraction is smaller than the denominator, the fraction is called proper fraction.
Improper Fraction
If the numerator of a fraction is greater than the denominator, the fraction is called improper fraction.
Mixed Fraction
Mixed fraction is the sum of a whole number and a proper fraction. Both the whole number and the fraction are written together, but the sign of the addition (+) does not appear between them.
Equivalent Fractions
Two or more fractions are said to be equivalent fractions, if they have the same value. In other words, when equivalent fractions are reduced into their simplest form, they give the same fraction.
Comparison of Unit Fractions
If the numerators of two fractions are same and their denominators are different, then the fractions having smaller denominator will be the greater one. To take an example, \[\frac{1}{P}\] and \[\frac{1}{Q}\] are unit fractions where p and Q are natural numbers. If \[Q<P\]then \[\frac{1}{p}<\frac{1}{Q}\].
Compare between \[\frac{1}{13}\] and \[\frac{1}{15}\]. which fraction is greater than other?
Solution: \[\frac{1}{13}>\frac{1}{15}\]
Because\[13<15\], therefore \[\frac{1}{13}>\frac{1}{15}\].
Comparison of Like Fractions
To compare unlike fractions, unlike fractions are converted into like fractions. Conversion is done by multiplying the numerator and denominator of both the fractions by a suitable numbers, such numbers, such that, denominators become equal.
Compare between \[\frac{5}{8}\] and \[\frac{3}{5}\]. Which fraction is the greater?
Solution: \[\frac{5}{8}>\frac{3}{5}\]
\[\frac{5}{8}\times \frac{5}{5}=\frac{25}{40}\] and \[\frac{3}{5}\times \frac{8}{8}=\frac{24}{40}\]
Since \[\frac{25}{40}>\frac{24}{40},\]therefore, \[\frac{5}{8}>\frac{3}{5}\].
Conversion of improper Fraction into mixed Fraction
If \[\frac{a}{b}\] is an improper fraction, then divide a by b by long division method. The mixed fraction equivalent to improper fraction is \[Q\frac{R}{b}\], where
Q = Quotient of \[\frac{a}{b}\]
R = Remainder left after \[\frac{a}{b}\].
Convert \[\frac{48}{5}\]into mixed fraction.
Solution: 
\[\therefore \]\[\frac{48}{5}=9\frac{3}{5}\]
Conversion of mixed fraction, then its equivalent fraction
If \[a\frac{b}{c}\] is mixed fraction, then its equivalent fraction is\[\frac{a\times c+b}{c}\].
Convert \[11\frac{1}{3}\] into improper fraction.
Solution: \[11\frac{1}{3}\]= \[\frac{11\times 3+1}{3}=\frac{33+1}{3}=\frac{34}{3}\]
You need to login to perform this action.
You will be redirected in
3 sec
