Fractions
Category : 5th Class
Fractions
A fraction is a part of whole. Fraction = \[\frac{\text{Numerator}}{\text{Denominator}}\]
In \[\frac{6}{7}\], 6 is called numerator and 7 is called denominator.
The denominator denotes the number of equal parts the whole is divided into.
The numerator denotes the number of parts considered of the whole.
Like fractions: Fractions with same denominators.
e.g., \[\frac{4}{5},\frac{6}{5},\frac{3}{5}\] etc.
Unlike fractions: Fractions with different denominators.
e.g.,\[\frac{1}{2},\frac{6}{8},\frac{9}{4}\] etc.
Proper fractions: Fractions in which the denominator is greater than the numerator.
e.g., \[\frac{2}{9},\frac{5}{6},\frac{3}{2}\] etc.
Improper fractions: Fractions in which the numerator is greater than the denominator.
e.g., \[\frac{9}{2},\frac{6}{5},\frac{2}{3}\]etc.
Mixed Number: A number with a whole number part and a fractional part is called a mixed number
e.g., \[1\frac{1}{2},2\frac{1}{3},3\frac{1}{4}\] etc.
e.g., convert \[\frac{13}{5}\] into a mixed number.
Solution: Divide -r and write in the form of\[\text{Q}\frac{\text{R}}{\text{D}}\], where Q = Quotient, R = Remainder and D = Denominator (Divisor).
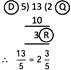
e.g., convert \[\text{3}\frac{1}{4}\] into an improper fraction.
Solution: Comparing \[\text{3}\frac{1}{4}\]with\[\text{Q}\frac{\text{R}}{\text{D}}\], Q = 3, R = 1 and D = 4.
∴ The required improper fraction
\[\text{=}\frac{\text{Q}\times \text{D}+\text{R}}{\text{D}}=\frac{\text{3}\times 4+1}{\text{4}}=\frac{13}{4}\]
All fractions that have the same value are called equivalent fractions. Equivalent fractions of a given fraction are obtained by multiplying or dividing both numerator and denominator by the same number.
e.g., \[\frac{1}{2},\frac{5}{10},\frac{11}{22}\] etc.
If the cross products of two fractions are equal, they are equivalent.
e.g.. (a) \[\frac{3}{4},\frac{75}{100}\]
![]()
3×100 = 300 and 75×4=300
is equivalent to \[\frac{75}{100}\]
e.g. (b) \[\frac{1}{5},\frac{2}{3}\]
1×3=3 and 2×5=10
3 ≠ 10
∴ \[\frac{1}{5}\] is not equivalent to\[\frac{2}{3}\].
Reducing a fraction to its lowest terms is called simplifying the fraction. Dividing the numerator and the denominator of a fraction by a factor common to both of them reduces it into its lowest terms.
A fraction is said to be in its lowest terms if its numerator and denominator have no common factor other than 1.
A fraction can be reduced to its lowest terms by cancelling the factors common to both numerator and denominator.
Lowest terms of a fraction can be found by dividing the numerator and denominator by their H.C.F.
e.g., Find the lowest terms of\[\frac{18}{30}\].
Solution: The H.C.F. of 18 and 30 is 6.
∴ \[\frac{18}{30}=\frac{18\div 6}{30\div 6}=\frac{3}{5}\]
Among the like fractions, a fraction with greater numerator is the greater fraction to compare unlike fractions, first convert them into equivalent fractions and then compare them.
While comparing fractions with the same numerators, the fraction with greater denominator is smaller.
Ordering fractions:
Ascending order: Fractions written in order from the smallest to the greatest are said to be in ascending order.
e.g., \[\frac{1}{5},\frac{1}{3},\frac{1}{2}\] are fractions in ascending order.
Descending order: Fractions written in order from the greatest to the smallest are said to be in descending order.
e.g., \[\frac{1}{2},\frac{1}{4},\frac{1}{5}\]- are fractions in descending order.
Add the numerators and write the sum on the same denominator.
e.g., \[\frac{7}{8}+\frac{3}{8}+\frac{12}{8}=\frac{7+3+12}{8}=\frac{22}{8}=\frac{11}{4}=2\frac{3}{4}\]
Convert the unlike fractions into like fractions with the common denominator (which is the L.C.M. of given denominators). Then add the numerators and write the sum on the same denominator.
e.g., \[\frac{3}{5}+\frac{2}{3}=\frac{3\times 3+2\times 5}{15}=\frac{9+10}{15}=\frac{19}{15}=1\frac{4}{15}\]
Two mixed numbers can be added by adding whole numbers and fractions separately.
e.g., \[2\frac{1}{3}+3\frac{1}{4}=(2+3)\left( \frac{1}{3}+\frac{1}{4} \right)=5+\left( \frac{4+3}{12} \right)=5\frac{7}{12}\]
If the sum of two fractions is not in lowest terms, it must be reduced to the lowest terms.
Like fractions are subtracted by finding the difference of numerators.
e.g., \[\frac{7}{15}-\frac{9}{15}=\frac{7-3}{15}=\frac{4}{15}\]
Unlike fractions are converted to like fractions and then subtracted.
e.g., \[\frac{9}{4}-\frac{3}{2}=\frac{18-12}{8}=\frac{6}{8}=\frac{3}{4}\]
If the difference of two fractions is not in its lowest terms, it must be reduced to the lowest terms.
To get the product of a fraction and a whole number, multiply the numerator of the fraction with the whole number. Factors common to numerator and denominator can be cancelled.
e.g., \[\frac{1}{2}\times 5=\frac{5}{2}\]
To get the product of two fractions, numerators and denominators are multiplied separately. Factors common to numerator and denominator are cancelled.
e.g., \[\frac{1}{3}\times \frac{2}{5}=\frac{1\times 2}{3\times 5}=\frac{2}{15}\]
When a fraction is multiplied by 1, the product is the fraction itself.
e.g., \[\frac{3}{4}\times 1=\frac{3}{4}\]
When a fraction is multiplied by 0, the product is 0.
e.g., \[\frac{2}{3}\times 0=0\]
To find the fraction of a quantity, the fraction and the number (quantity) are multiplied and simplified.
e.g., \[\frac{1}{3}\]of Rs 90 = \[\frac{1}{3}\]× Rs 90 = Rs 30
Interchanging the numerator and denominator of a fraction results in its reciprocal
e.g., \[\frac{3}{2}\]is the reciprocal of\[\frac{2}{3}\].
Note: Two numbers are the multiplicative inverses of each other if their product is 1.
Dividing a fraction by another fraction is to multiply the fraction by the reciprocal of the other.
e.g., \[\frac{2}{3}\div \frac{6}{8}=\frac{2}{3}\times \frac{8}{6}=\frac{8}{3\times 3}=\frac{8}{9}\]
When a fraction is divided by 1, the quotient is the fraction itself.
e.g., \[\frac{3}{4}\div 1=\frac{3}{4}\]
When 1 is divided by a fraction, the quotient is the reciprocal of the fraction.
e.g., \[1\div \frac{3}{4}=\frac{4}{3}\]
When 0 is divided by a fraction, the quotient is 0.
e.g., \[0\div \frac{3}{6}\]
Note: Division of a fraction by 0 is not defined as division by 0 is not defined.
When a fraction is multiplied by its reciprocal, the product is 1.
e.g., \[\frac{3}{4}\times \frac{4}{3}=1\]
When a fraction is divided by itself, the quotient is 1.
e.g., \[\frac{2}{3}\div \frac{2}{3}=1\]
Note: Division of a fraction by 0 is not defined as division by 0 is not defined.
When a fraction is multiplied by its reciprocal, the product is 1.
e.g., \[\frac{3}{4}\times \frac{4}{3}=1\]
When a fraction is divided by itself, the quotient is 1.
e.g., \[\frac{2}{3}\div \frac{2}{3}=1\]
You need to login to perform this action.
You will be redirected in
3 sec
