-
question_answer1) From an external point P, tangents PA and PB are drawn to a circle with centre O. If \[\angle PAB=50{}^\circ \], then find \[\angle AOB.\]
View Answer play_arrow
-
question_answer2)
| In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of \[60{}^\circ \] to the horizontal and reaches up to a point D of pole. If \[AD=2.54\text{ }m\], find the length of the ladder. (Use \[\sqrt{3}=1.73\]) |
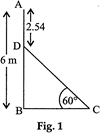 |
View Answer play_arrow
-
question_answer3) Find the 9th term from the end (towards the first term) of the A.P 5, 9, 13,......, 185.
View Answer play_arrow
-
question_answer4) Cards marked with number 3, 4, 5,......, 50 are placed in a box and mixed thoroughly. A card is drawn at random from the box. Find the probability that the selected card bears a perfect square number.
View Answer play_arrow
-
question_answer5) If \[x=\frac{2}{3}\] and \[x=-3\] are roots of the quadratic equation \[a{{x}^{2}}+7x+b=0\], find the values of a and b.
View Answer play_arrow
-
question_answer6) Find the ratio in which y-axis divides the line segment joining the points \[A(5,-6)\] and \[B(-1,-4)\]. Also find the coordinates of the point of division.
View Answer play_arrow
-
question_answer7)
| In Fig. 2, a circle is inscribed in a \[\Delta \,ABC\], such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF. |
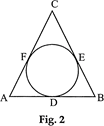 |
View Answer play_arrow
-
question_answer8) The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from \[Q(2,-5)\]and \[R(-3,6)\], find the coordinates of P.
View Answer play_arrow
-
question_answer9) How many terms of the A.P. 18, 16, 14, ?. Be so that their sum is zero?
View Answer play_arrow
-
question_answer10)
| In Fig. 3, AP and BP are tangents to a circle with centre O, such that \[AP=5\text{ }cm\] and \[\angle APB=60{}^\circ \]. Find the length of chord AB. |
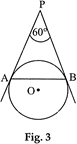 |
View Answer play_arrow
-
question_answer11)
| In Fig. 4, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region, \[\left( use\,\pi =\frac{22}{7} \right)\] |
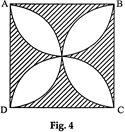 |
View Answer play_arrow
-
question_answer12)
| In Fig. 5, is a decorative block, made up of two solids - a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has a diameter of 3.5 cm. Find the total surface area of the block, use \[\left( use\,\,\pi =\frac{22}{7} \right)\] |
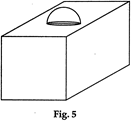 |
View Answer play_arrow
-
question_answer13)
| In Fig. 6, ABC is a triangle coordinates of whose vertex A are (\[0,\text{ }1\]). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of \[\Delta \text{ }ABC\] and \[\Delta \text{ }DEF\] . |
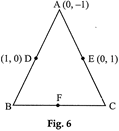 |
View Answer play_arrow
-
question_answer14)
| In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ as diameter with centre M. If \[OP=PQ=10\text{ }cm\] show that area of shaded region is 25\[\left( \sqrt{3}-\frac{\pi }{6} \right)c{{m}^{2}}\]. |
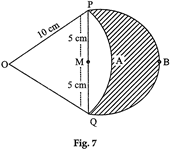 |
View Answer play_arrow
-
question_answer15) If the sum of first 7 terms of an A.P. is 49 and that of its first 17 terms is 289, find the sum of first n terms of the A.P.
View Answer play_arrow
-
question_answer16) Solve for x: \[\frac{2x}{x-3}+\frac{1}{2x+3}+\frac{3x+9}{(x-3)(2x+3)}=0,x\ne 3,-3/2\]
View Answer play_arrow
-
question_answer17) A well of diameter 4 m is dug 21 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 3 m to form an embankment. Find the height of the embankment.
View Answer play_arrow
-
question_answer18) The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder,\[\left( use\,\pi =\frac{22}{7} \right)\]
View Answer play_arrow
-
question_answer19) The angles of depression of the top and bottom of a 50 m high building from the top of a tower are \[45{}^\circ \] and \[60{}^\circ \] respectively. Find the height of the tower and the horizontal distance between the tower and the building, (use \[\sqrt{3}=1.73\])
View Answer play_arrow
-
question_answer20)
| In a single throw of a pair of different dice, what is the probability of getting |
| (i) a prime number on each dice? |
| (ii) a total of 9 or 11? |
View Answer play_arrow
-
question_answer21) A passenger, while boarding the plane, slipped from the stairs and got hurt. The pilot took the passenger in the emergency clinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/hour than the usual speed. Find the usual speed of the plane. What value is depicted in this question?
View Answer play_arrow
-
question_answer22) Prove that the lengths of tangents drawn from an external point to a circle are equal.
View Answer play_arrow
-
question_answer23) Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length.
View Answer play_arrow
-
question_answer24)
| In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that \[OT=13\text{ }cm\] and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle. |
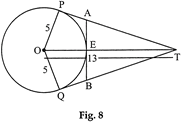 |
View Answer play_arrow
-
question_answer25) Find x in terms of a, b and c: \[\frac{a}{x-a}+\frac{b}{x-b}=\frac{2c}{x-c},x\ne a,b,c\]
View Answer play_arrow
-
question_answer26) A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is \[45{}^\circ \]. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is \[30{}^\circ \]. Find the speed of flying of the bird. (Take \[\sqrt{3}=1.732\])
View Answer play_arrow
-
question_answer27) A thief runs with a uniform speed of 100 m/minute. After one minute a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 W minute every succeeding minute. After how many minutes the policeman will catch the thief.
View Answer play_arrow
-
question_answer28) Prove that the area of a triangle with vertices \[(t,t-2),(t+2,t+2)\] and \[(t+3,t)\] is independent of t.
View Answer play_arrow
-
question_answer29)
| A game of chance consists of spinning an arrow on a circular board, divided into 8 equal parts, which comes to rest pointing at one of the numbers 1, 2, 3,..., 8 (Fig. 9), which are equally likely outcomes. What is the probability that the arrow will point at (i) an odd number, (ii) a number greater than 3, (iii) a number less than 9. |
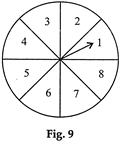 |
View Answer play_arrow
-
question_answer30)
| An elastic belt is placed around the rim of a pulley of radius 5 cm. (Fig. 10) From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also find the shaded area. (use \[\pi =3.14\] and \[\sqrt{3}=1.73\]) |
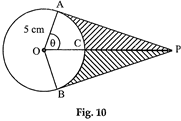 |
View Answer play_arrow
-
question_answer31) A bucket open at the top is in the form of frustum of a cone with a capacity of \[12308.8\text{ }c{{m}^{3}}\]. The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use \[\pi =3.14\])
View Answer play_arrow










