question_answer

The angles of depression of the top and bottom of a 50 m high building from the top of a tower are \[45{}^\circ \] and \[60{}^\circ \] respectively. Find the height of the tower and the horizontal distance between the tower and the building, (use \[\sqrt{3}=1.73\])

Answer:

Let AB and CD be the tower and high building respectively

Given,               \[CD=50\text{ }m\]

Let,                   \[AB=h\text{ }m\]

Then, in \[\Delta \,ADE\]

\[\tan \,45{}^\circ =\frac{AE}{DE}\]

\[1=\frac{h-50}{DE}\]

\[DE=h-50\]                                      ?(i)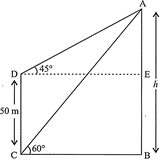

and, in \[\Delta \text{ }ACB\]

\[\tan \,60{}^\circ =\frac{AB}{CB}\]

\[\sqrt{3}=\frac{h}{CB}\]

\[CB=\frac{h}{\sqrt{3}}\]                                          ?(ii)

Now, \[CB=DE\]

then from eq. (i) and (ii), we get

\[h-50=\frac{h}{\sqrt{3}}\]

\[h-\frac{h}{\sqrt{3}}=50\]

\[\frac{\left( \sqrt{3}-1 \right)}{\sqrt{3}}h=50\]

\[h=\frac{50\sqrt{3}}{\sqrt{3}-1}=\frac{50\sqrt{3}}{\sqrt{3}-1}\times \frac{50\sqrt{3}}{\sqrt{3}-1}\]

\[=25\times 3+25\sqrt{3}\]

\[h=75+25(1.73)\]

\[=118.25\,m\]

Hence, the height of the tower is \[118.25\text{ }m\]and the horizontal distance between the tower and the building is\[68.25\text{ }m\].