| Direction: A point object O is placed at the origin of coordinate system. An equi-convex thin lens\[({{\mu }_{g}}=1.5)\] of focal length \[f=20\,cm\]in air is placed so that its principal axis is along x-axis. Now the lens is cut at the middle (along the principal axis) and upper half is shifted along x-axis and y-axis by 20 cm and 2 mm respectively and right side of lower half is filled with water \[({{\mu }_{\omega }}=4/3)\] |
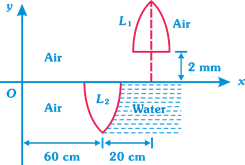 |
| Coordinates of the image produced by the lens \[{{L}_{1}}\] will be |
A) \[\left( \frac{320}{3}cm,\frac{4}{3}mm \right)\]
B) \[\left( \frac{160}{3}cm,\frac{8}{3}mm \right)\]
C) \[\left( \frac{320}{3}cm,\frac{8}{3}mm \right)\]
D) \[\left( \frac{160}{3}cm,\frac{4}{3}mm \right)\]
Correct Answer: C
Solution :
| [c] Given, \[f=20\text{ }cm\] |
| \[\therefore \] \[m=\frac{v}{u}\] |
| Now, \[u=-80\,cm\] |
| \[\therefore \] \[v=\frac{uf}{u+f}=\frac{80}{3}\,cm\] |
| \[\left( \text{As},\text{ lens formula is}\,\,\frac{1}{v}-\frac{1}{u}=\frac{1}{f} \right)\] |
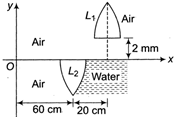 |
| \[\therefore \] x-coordinate \[=80+\frac{80}{3}=\frac{320}{3}\,cm\] |
| \[\therefore \] y-coordinatemm \[=\left( \frac{2}{3}+2 \right)mm=\frac{8}{3}\,mm\] |
| Hence, coordinates of image formed by \[{{L}_{1}}=\left( \frac{320}{3}cm,\frac{8}{3}mm \right)\] |
You need to login to perform this action.
You will be redirected in
3 sec
