| (i) Derive the lens formula \[\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\] for a concave lens, using the necessary ray diagram. |
| (ii) The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 4 m away by means of a large convex lens. What is the maximum possible focal length of the lens required for this purpose? |
| Or |
| Figure below shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 50 cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0 cm. What is the refractive index of the liquid? |
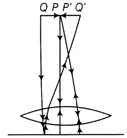
Answer:
(i) The formation of image by a concave lens L is shown in figure below. 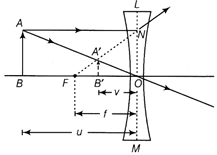 Ray diagram of concave lens Consider AB as an object and A' B' is its image. The object is at a distance u from the lens and its image is formed at a distance v. Triangles ABO and A'B'0 are similar, \[\therefore \] \[\frac{AB}{A'B'}=\frac{OB}{OB'}\] ?(i) Also, triangles NOF and A' B' F are similar, \[\frac{NO}{A'B'}=\frac{OF}{FB'}\] But NO = AB \[\therefore \] \[\frac{AB}{A'B'}=\frac{OF}{FB'}\] Comparing Eqs. (i) and (ii), we get \[\frac{OB}{OB'}=\frac{OF}{FB'}\Rightarrow \frac{OB}{OB'}=\frac{OF}{OF-OB'}\] Using sign conventions of coordinate geometry. Let, \[OB=-u,\] \[OB'=-v,\] \[OF=-f\] \[\therefore \] \[\frac{-u}{-v}=\frac{-f}{-f+v}\] or \[uf-uv=vf\] or \[uv=uf-vf\] Dividing throughout by uvf, we get \[\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\] This is the required lens formula. (ii) Let x be the distance between the object and the image. Given x = 4m. Here \[u+y=x\] According to lens formula \[\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\Rightarrow \frac{1}{\left| u \right|}=\frac{1}{f}-\frac{1}{v}=\frac{v-f}{vf}\] or \[\left| u \right|=\frac{vf}{v-f}\] \[x=u+v=\frac{vf}{v-f}+v=\frac{vf+v(v-f)}{v-f}\] \[\Rightarrow (v-f)x={{v}^{2}}\Rightarrow {{v}^{2}}-vx+xf=0\] The solution for this quadratic equation is \[v=\frac{x\pm \sqrt{{{2}^{2}}-4fx}}{2}\] For real image, v must be positive i.e. \[{{x}^{2}}-4fx\ge 0\] \[\Rightarrow \] \[{{x}^{2}}\ge 4fx\] \[x\ge 4f\Rightarrow f\le \frac{x}{4}\] The maximum value of f is \[\frac{x}{4}=\frac{4}{4}=1m\] Or Distance of the needle from the lens in the first case = Focal length F of the combination of the convex lens and plano-concave lens formed by the liquid i.e. F = 50 cm Distance measured in second case = Focal length of the convex lens i.e. \[{{f}_{1}}=+30\,cm\] The focal length \[{{f}_{2}}\] of the plano-concave lens is given by \[\frac{1}{{{f}_{1}}}+\frac{1}{{{f}_{2}}}=\frac{1}{F}\] or \[\frac{1}{{{f}_{2}}}=\frac{1}{F}-\frac{1}{{{f}_{1}}}=\frac{1}{50}-\frac{1}{30}=\frac{3-5}{150}\] \[\Rightarrow \] \[\frac{1}{{{f}_{2}}}=\frac{-2}{150}\] \[\therefore \] \[{{f}_{2}}=-75\,cm\] Now, for the equiconvex lens, we have \[{{R}_{1}}=R,\] \[{{R}_{2}}=-R,\] \[f=30\,cm,\] \[\mu =1.5\] Using lens maker's formula, \[\frac{1}{f}=(\mu -1)\left[ \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right]\] or \[\frac{1}{30}=(1.5-1)\left[ \frac{1}{R}+\frac{1}{R} \right]=0.5\times \frac{2}{R}\] or \[R=0.5\times 2\times 30\,cm=30\,cm\] For plano-convex lens, \[f=-75\,cm\] For concave surface, \[{{R}_{1}}=-R=-30\,cm\] For plane surface, \[{{R}_{2}}=\infty \] As, \[\frac{1}{f}=(\mu -1)\left[ \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right]\] \[\frac{1}{-75}=(\mu -1)\left[ \frac{1}{-30}-\frac{1}{\infty } \right]\] or \[\mu -1=\frac{-30}{-75}=\frac{3}{5}\] or \[\mu =1+\frac{3}{5}=\frac{8}{5}\Rightarrow \mu =1.6\]
Ray diagram of concave lens Consider AB as an object and A' B' is its image. The object is at a distance u from the lens and its image is formed at a distance v. Triangles ABO and A'B'0 are similar, \[\therefore \] \[\frac{AB}{A'B'}=\frac{OB}{OB'}\] ?(i) Also, triangles NOF and A' B' F are similar, \[\frac{NO}{A'B'}=\frac{OF}{FB'}\] But NO = AB \[\therefore \] \[\frac{AB}{A'B'}=\frac{OF}{FB'}\] Comparing Eqs. (i) and (ii), we get \[\frac{OB}{OB'}=\frac{OF}{FB'}\Rightarrow \frac{OB}{OB'}=\frac{OF}{OF-OB'}\] Using sign conventions of coordinate geometry. Let, \[OB=-u,\] \[OB'=-v,\] \[OF=-f\] \[\therefore \] \[\frac{-u}{-v}=\frac{-f}{-f+v}\] or \[uf-uv=vf\] or \[uv=uf-vf\] Dividing throughout by uvf, we get \[\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\] This is the required lens formula. (ii) Let x be the distance between the object and the image. Given x = 4m. Here \[u+y=x\] According to lens formula \[\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\Rightarrow \frac{1}{\left| u \right|}=\frac{1}{f}-\frac{1}{v}=\frac{v-f}{vf}\] or \[\left| u \right|=\frac{vf}{v-f}\] \[x=u+v=\frac{vf}{v-f}+v=\frac{vf+v(v-f)}{v-f}\] \[\Rightarrow (v-f)x={{v}^{2}}\Rightarrow {{v}^{2}}-vx+xf=0\] The solution for this quadratic equation is \[v=\frac{x\pm \sqrt{{{2}^{2}}-4fx}}{2}\] For real image, v must be positive i.e. \[{{x}^{2}}-4fx\ge 0\] \[\Rightarrow \] \[{{x}^{2}}\ge 4fx\] \[x\ge 4f\Rightarrow f\le \frac{x}{4}\] The maximum value of f is \[\frac{x}{4}=\frac{4}{4}=1m\] Or Distance of the needle from the lens in the first case = Focal length F of the combination of the convex lens and plano-concave lens formed by the liquid i.e. F = 50 cm Distance measured in second case = Focal length of the convex lens i.e. \[{{f}_{1}}=+30\,cm\] The focal length \[{{f}_{2}}\] of the plano-concave lens is given by \[\frac{1}{{{f}_{1}}}+\frac{1}{{{f}_{2}}}=\frac{1}{F}\] or \[\frac{1}{{{f}_{2}}}=\frac{1}{F}-\frac{1}{{{f}_{1}}}=\frac{1}{50}-\frac{1}{30}=\frac{3-5}{150}\] \[\Rightarrow \] \[\frac{1}{{{f}_{2}}}=\frac{-2}{150}\] \[\therefore \] \[{{f}_{2}}=-75\,cm\] Now, for the equiconvex lens, we have \[{{R}_{1}}=R,\] \[{{R}_{2}}=-R,\] \[f=30\,cm,\] \[\mu =1.5\] Using lens maker's formula, \[\frac{1}{f}=(\mu -1)\left[ \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right]\] or \[\frac{1}{30}=(1.5-1)\left[ \frac{1}{R}+\frac{1}{R} \right]=0.5\times \frac{2}{R}\] or \[R=0.5\times 2\times 30\,cm=30\,cm\] For plano-convex lens, \[f=-75\,cm\] For concave surface, \[{{R}_{1}}=-R=-30\,cm\] For plane surface, \[{{R}_{2}}=\infty \] As, \[\frac{1}{f}=(\mu -1)\left[ \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right]\] \[\frac{1}{-75}=(\mu -1)\left[ \frac{1}{-30}-\frac{1}{\infty } \right]\] or \[\mu -1=\frac{-30}{-75}=\frac{3}{5}\] or \[\mu =1+\frac{3}{5}=\frac{8}{5}\Rightarrow \mu =1.6\]
You need to login to perform this action.
You will be redirected in
3 sec
