| An alternating emf \[E={{E}_{0}}\sin \omega t\] is applied as an input in a purely resistive circuit of resistance R. |
| (i) What is the current in the circuit? |
| (ii) What is the phase difference between the emf and the current? |
| (iii) Draw the graphical representation of the emf and the current. |
| (iv) What is the average power dissipated? |
| (v) Show the emf and current in vector representation. |
| Or |
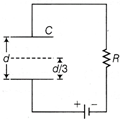
| What is time constant? A parallel plate capacitor of capacitance C with plates of unit area and separation d is filled with a liquid of dielectric constant K = 2. The level of liquid is \[\frac{d}{3}\] initially. Suppose the liquid level decreases at a constant speed v. What will be the time constant as a function of time t? |
 |
Answer:
(i) Alternating emf, \[E={{E}_{0}}\sin \omega t\] \[\therefore \] Current in the circuit, \[I=\frac{E}{R}=\frac{{{E}_{0}}}{R}\sin \omega t\] or \[I={{I}_{0}}\sin \omega t\] where, \[{{I}_{0}}=\frac{{{E}_{0}}}{R}\] is the peak value of current.
(ii) Phase difference between the emf and the current is zero.
(iii) Graphical representation of the emf and the current.
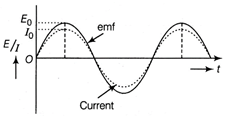 Graphical representation of the emf and current (iv) Average power dissipated in the circuit, \[\overline{P}={{E}_{rms}}{{I}_{rms}}\cos \phi \] Here, \[\phi =0{}^\circ \] and \[{{E}_{rms}}=\frac{{{E}_{0}}}{\sqrt{2}}\] and \[{{I}_{rms}}=\frac{{{I}_{0}}}{\sqrt{2}}=\frac{{{E}_{0}}}{\sqrt{2}R}\] \[\therefore \] \[\overline{P}=\frac{{{E}_{0}}}{\sqrt{2}}\times \frac{{{E}_{0}}}{\sqrt{2}R}\cos \,0{}^\circ =\frac{E_{0}^{2}}{2R}\] (v) Emf and current in vector representation is shown below:
Graphical representation of the emf and current (iv) Average power dissipated in the circuit, \[\overline{P}={{E}_{rms}}{{I}_{rms}}\cos \phi \] Here, \[\phi =0{}^\circ \] and \[{{E}_{rms}}=\frac{{{E}_{0}}}{\sqrt{2}}\] and \[{{I}_{rms}}=\frac{{{I}_{0}}}{\sqrt{2}}=\frac{{{E}_{0}}}{\sqrt{2}R}\] \[\therefore \] \[\overline{P}=\frac{{{E}_{0}}}{\sqrt{2}}\times \frac{{{E}_{0}}}{\sqrt{2}R}\cos \,0{}^\circ =\frac{E_{0}^{2}}{2R}\] (v) Emf and current in vector representation is shown below: 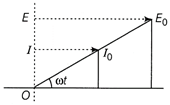 Or A time constant in capacitor or inductor is fall and raise of current with respect to time. It is concerned with switching speed of capacitor/inductor. A time constant is denoted by \[\tau \] or T. If internal resistance of capacitor/inductor is R than time constant is CR or L/R. According to question, after time t, thickness of liquid inside the capacitor will remains \[\left( \frac{d}{3}-vt \right)\] Now, as we know that time constant is equals to CR. i.e. \[\tau =CR=\frac{{{\varepsilon }_{0}}R}{\left( d-\frac{d}{3}+vt \right)+\left( \frac{d/3-vt}{2} \right)}\] \[\left[ Applying\,C=\frac{{{\varepsilon }_{0}}A}{\left( d-t+\frac{t}{K} \right)} \right]\] \[=6{{\varepsilon }_{0}}R/5d+3vt\] [Given, A = 1] So, at time t the time constant \[\tau \] is given by \[\frac{6{{\varepsilon }_{0}}R}{5d+3\,vt}.\]
Or A time constant in capacitor or inductor is fall and raise of current with respect to time. It is concerned with switching speed of capacitor/inductor. A time constant is denoted by \[\tau \] or T. If internal resistance of capacitor/inductor is R than time constant is CR or L/R. According to question, after time t, thickness of liquid inside the capacitor will remains \[\left( \frac{d}{3}-vt \right)\] Now, as we know that time constant is equals to CR. i.e. \[\tau =CR=\frac{{{\varepsilon }_{0}}R}{\left( d-\frac{d}{3}+vt \right)+\left( \frac{d/3-vt}{2} \right)}\] \[\left[ Applying\,C=\frac{{{\varepsilon }_{0}}A}{\left( d-t+\frac{t}{K} \right)} \right]\] \[=6{{\varepsilon }_{0}}R/5d+3vt\] [Given, A = 1] So, at time t the time constant \[\tau \] is given by \[\frac{6{{\varepsilon }_{0}}R}{5d+3\,vt}.\]
You need to login to perform this action.
You will be redirected in
3 sec
