question_answer

In the circuit shown in figure, when the input voltage for the base resistance is 10 V. \[{{V}_{BE}}\] is zero and \[{{V}_{CE}}\] is also zero. Find the values of \[{{I}_{B}},\] \[{{I}_{C}}\] and \[\beta .\]

Answer:

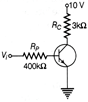
As \[{{V}_{BE}}=0,\] potential drop across \[{{R}_{B}}\] is 10 V. \[\therefore \]      \[{{I}_{B}}=\frac{10}{400\times {{10}^{3}}}=25\mu A=25\times {{10}^{-6}}A\]                                     \[(\because {{V}_{i}}-{{V}_{BE}}={{I}_{B}}{{R}_{B}})\] Since, \[{{V}_{CE}}=0,\] potential drop across \[{{R}_{C}},\]i.e. \[{{I}_{C}}{{R}_{C}}\] is 10 V. \[\therefore \]      \[{{I}_{C}}=\frac{10}{3\times {{10}^{3}}}=3.33\times {{10}^{-3}}=3.33mA\]                                     \[(\because {{V}_{CC}}-{{V}_{CE}}={{I}_{C}}{{R}_{C}})\] \[\therefore \]      \[\Beta =\frac{{{I}_{C}}}{{{I}_{B}}}=\frac{3.33\times {{10}^{-3}}}{25\times {{10}^{-6}}}=1.33\times {{10}^{2}}=133\]