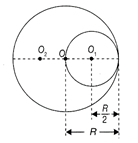
A) \[\frac{R}{7}\]
B) \[\frac{R}{14}\]
C) \[\frac{R}{2}\]
D) \[R\]
Correct Answer: B
Solution :
Let \[\rho \]by the density of lead. Then M\[M=\frac{4}{3}\pi {{r}^{3}}p=\]mass of total sphere \[{{m}_{1}}=\frac{4}{3}\pi {{\left( \frac{R}{2} \right)}^{3}}\rho =\] Mass of removed part \[=\frac{M}{8}\] \[{{m}_{2}}=M-\frac{M}{8}=\frac{7M}{8}=\]Mass of remaining sphere choosing the centre of the sphere as the origin. \[{{x}_{cm}}=\frac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}\]or, \[o=\frac{\frac{M}{8}\times \frac{R}{2}+\frac{7M}{8}{{x}_{2}}}{M}\]or \[{{x}_{2}}=-\frac{R}{14}\,\,\therefore \]Shift in centre of mass\[=R/14.\] Hence, the correction option is (b).You need to login to perform this action.
You will be redirected in
3 sec
