Answer:
Let ABCD be the trapezium such that AB = 40 cm and CD = 20 cm and AD = BC = 26 cm. 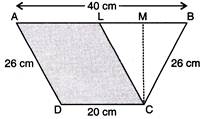
Now, draw CL || AD Then, ALCD is a parallelogram So, AL=CD=20cmandCL=AD=26cm. In\[\Delta CLB\], we have CL = CB = 26 cm Therefore, \[\Delta CLB\]is an isosceles triangle. Draw altitude CM of \[\Delta CLB.~\] Since \[\Delta CLB\] is an isosceles triangle. So, CM is also the median. Then, LM = \[MB=\frac{1}{2}BL=\frac{1}{2}\text{ }\times 20cm=10cm\] [as BL = AB -AL = (40 - 20) cm = 20 cm]. Applying Pythagoras theorem in \[\Delta CLM,\] we have, \[C{{L}^{2}}=C{{M}^{2}}+L{{W}^{2}}\] \[{{26}^{2}}=C{{M}^{2}}+\text{1}{{\text{0}}^{2}}\] \[C{{M}^{2}}={{26}^{2}}-{{10}^{2}}\] \[=\left( 26-10 \right)\left( 26+10 \right)\] \[=16\times 36=576\] CM = \[\sqrt{576}\] = 24 cm Hence, the area of the trapezium\[=\frac{1}{2}\times \] (sum of parallel sides) \[\times \] Height \[=\frac{1}{2}(20+40)\times 24\] \[=30\times 24=720\text{ }c{{m}^{2}}~\]
You need to login to perform this action.
You will be redirected in
3 sec
