| Find the equation of the plane passing through the line of intersection of planes |
| \[2x+y-z=3,\] \[5x-3y+4z+9=0\] and parallel to the line \[\frac{x-1}{2}=\frac{y-3}{4}=\frac{z-5}{5}.\] |
| OR |
| Find the distance of the point \[(-\,2,\,\,3,\,\,-4)\] from the line \[\frac{x+2}{3}=\frac{2y+3}{4}=\frac{3z+4}{5}\] measured parallel to the plane \[4x+12y-3z+1=0.\] |
Answer:
Given planes are\[2x+y-z=3\] ?(i) and \[5x-3y+4z+9=0\] ?(ii) Also, the given line is \[\frac{x-1}{2}=\frac{y-3}{4}=\frac{z-5}{5}\] ?(iii) Equation of any plane through the intersection of the planes (i) and (ii) is \[(2x+y-z-3)+\lambda \,(5x-3y+4z+9)=0\] \[\Rightarrow \]\[(2+5\lambda )\,x+(1-3\lambda )\,y+(4\lambda -1)\,z-(3-9\lambda )=0\] ?(iv) According to the question, plane (iv) is parallel to line (iii). \[\therefore \]\[(2+5\lambda )\cdot 2+(1-3\lambda )\cdot 4+(4\lambda -1)\cdot 5=0\] \[\Rightarrow \] \[18\lambda +3=0\Rightarrow \]\[\lambda =\frac{-\,1}{6}\] From Eq. (iv), we have \[\left( 2-\frac{5}{6} \right)x+\left( 1+\frac{1}{2} \right)y+\left( \frac{-\,2}{3}-1 \right)z-\left( 3+\frac{3}{2} \right)=0\] \[\Rightarrow \] \[7x+9y-10z-27=0\] Which is the required equation of plane. OR Given equation of line is \[\frac{x+2}{3}=\frac{2\left( y+\frac{3}{2} \right)}{4}=\frac{3\left( z+\frac{4}{3} \right)}{5}\] or \[\frac{x+2}{9}=\frac{y+\frac{3}{2}}{4}=\frac{3\left( z+\frac{4}{3} \right)}{5}\] 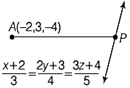
General point on line is \[P\left( 9\lambda -2,\,\,6\lambda -\frac{3}{2},\,\,5\lambda -\frac{4}{3} \right)\] ?(i) DR?s of AP are\[9\lambda -2+2,\]\[6\lambda -\frac{3}{2}-3,\]\[5\lambda -\frac{4}{3}+4\] i.e \[9\lambda ,\]\[6\lambda -\frac{9}{2},\]\[5\lambda +\frac{8}{3}\]. If AP is parallel to the plane\[4x+12y-3z+1=0\] Then, \[36\lambda +12\,\left( 6\lambda -\frac{9}{2} \right)-3\left( 5\lambda +\frac{8}{3} \right)=0\] \[\Rightarrow \]\[36\lambda +72\lambda -54-15\lambda -8=0\] \[\Rightarrow \]\[93\lambda -62=0\Rightarrow \lambda =\frac{2}{3}\] On putting the value of \[\lambda \]in Eq. (i), we get the point of intersection is \[P\,(6-2,\,\,4-\frac{3}{2},\,\,2)\], i.e. \[P\,\left( 4,\,\,\frac{5}{2},\,\,2 \right)\] \[\therefore \]Distance\[AP=\sqrt{{{(4+3)}^{2}}+{{\left( \frac{5}{2}-3 \right)}^{2}}+{{(2+4)}^{2}}}\] \[=\sqrt{36+\frac{1}{4}+36=}\sqrt{\frac{289}{4}}=\frac{17}{2}units\]
You need to login to perform this action.
You will be redirected in
3 sec
