| A large transparent cube (refractive index\[=1.5\]) has a small air bubble inside it. When a coin (diameter\[2\text{ }cm\]) is placed symmetrically above the bubble on the top surface of the cube, the bubble cannot be seen by looking down into the cube at any angle. However, when a smaller coin (diameter\[1.5cm\]) is placed directly over it, the bubble can be seen by looking down into the cube. What is the range of the possible depths d of the air bubble beneath the top surface? |
|
A) \[\frac{3\sqrt{5}}{8}cm<d<\frac{\sqrt{5}}{2}cm\]
B) \[\frac{2\sqrt{3}}{8}cm<d<\frac{3\sqrt{5}}{2}cm\]
C) \[\frac{\sqrt{5}}{7}cm<d<\frac{2\sqrt{5}}{7}cm\]
D) \[\frac{\sqrt{3}}{7}cm<d<\frac{3\sqrt{3}}{7}cm\]
Correct Answer: A
Solution :
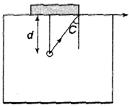
| [a] The depth of the bubble shall not be more than that shown in the figure, when the coin of diameter \[2\text{ }cm\]is placed above it. A larger depth will mean that that the angle of incidence at points not covered by the coin can be lesser than the critical angle [c]. |
| \[\mu \,\,\sin C=1\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\operatorname{tanC}=\frac{1}{\sqrt{{{\mu }^{2}}-1}}\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\operatorname{tanC}=\frac{2}{\sqrt{5}}\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{d}=\frac{2}{\sqrt{5}}\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,d=\frac{\sqrt{5}}{2}\] |
| The depth at which the bubble will be just visible if the smaller coin is placed can be similarly calculated as |
| \[\tan C=\frac{2}{\sqrt{5}}\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\frac{3/4}{d}=\frac{2}{\sqrt{5}}\] |
| \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,d=\frac{3\sqrt{5}}{8}\] |
| If the bubble happens to be below this depth, it will be certainly visible. |
 |
| Therefore, \[\frac{3\sqrt{5}}{8}<d<\frac{\sqrt{5}}{2}cm.\] |
You need to login to perform this action.
You will be redirected in
3 sec
