question_answer

In the figure shown XX represents a vertical plane perpendicular to the plane of the figure. To the right of this plane there is a uniform horizontal magnetic field B directed into the plane of the figure. A uniform electric field E exists horizontally perpendicular to the magnetic field in entire space. A charge particle having charge q and mass m is projected vertically upward from point 0. It crosses the plane XX after time T. Find the speed of projection of the particle if it was observed to move uniformly after time T. It is given that\[qE=mg\].

 

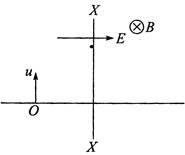
A) \[2gT\]  

B) \[gT\]

C) \[\frac{gT}{2}\]             

D) \[\frac{3gT}{\sqrt{2}}\]

Correct Answer: A

Solution :

[a] After crossing the XY plane, the forces on the particle are (1) \[mg\,(\downarrow )\] (2) \[qE(\to )\] (3) Magnetic force perpendicular to velocity \[({{F}_{B}}=qVB)\]. For particle to move uniformly, the magnetic force must balance the resultant of \[mg\] and \[qE\]. Hence, direction of velocity must be as shown in figure.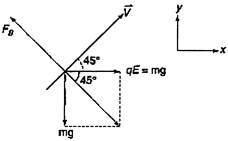 Component of velocity inland Y direction must be same. \[{{V}_{x}}={{V}_{y}}\] Since acceleration in y direction before entering magnetic field is a \[{{a}_{y}}=\frac{qE}{m}=\frac{mg}{m}=g,\] we have \[u-gT=gT\] \[u=2gT\]