-
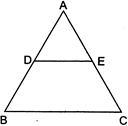
question_answer1)
Two polygons have same number of sides are similar, if:
A)
their corresponding sides are proportional done
clear
B)
their corresponding angles are equal done
clear
C)
both [a] and [b] done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer2)
Two figures having the same shape and no necessarily the same size are called:
A)
congruent figures done
clear
B)
equal figures done
clear
C)
similar figures done
clear
D)
symmetric figures done
clear
View Solution play_arrow
-
question_answer3)
The height of mountains is found out using the idea of indirect measurements which is based on the:
A)
principle of congruent figures done
clear
B)
principle of similarity of figures done
clear
C)
principle of equality of figures done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer4)
| If \[\Delta ABC\tilde{\ }\Delta PQR,\], then \[y+z\] equals: |
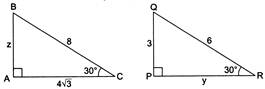 |
A)
\[2+\sqrt{3}\] done
clear
B)
\[4+3\sqrt{3}\] done
clear
C)
\[4+\sqrt{3}\] done
clear
D)
\[3+4\sqrt{3}\] done
clear
View Solution play_arrow
-
question_answer5)
| In the given figure,\[\Delta ACB\tilde{\ }\Delta APQ\]. If \[AB=6cm,\]\[BC=8cm\]and \[PQ=4cm,\]then \[AQ\]is equal to: |
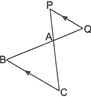 |
A)
\[2\,cm\] done
clear
B)
\[2.5\,cm\] done
clear
C)
\[3\,cm\] done
clear
D)
\[3.5\,cm\] done
clear
View Solution play_arrow
-
question_answer6)
If triangle \[\text{ABC}\] is similar to triangle \[\text{DEF}\] such that \[3AB=DE\]and \[\text{BC}=\text{9 cm},\]then \[\text{EF}\] is equal to:
A)
\[\text{27}\,\text{cm}\] done
clear
B)
\[\text{3 cm}\] done
clear
C)
\[\text{6 cm}\] done
clear
D)
\[\text{9 cm}\] done
clear
View Solution play_arrow
-
question_answer7)
| In a \[\Delta ABC,\] it is given that \[AB=6cm,\] \[\text{AC}=\text{8 cm}\] and \[\text{AD}\] is the bisector of \[\angle A\]. |
| Then, \[BD:DC=\] |
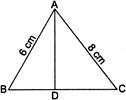 |
A)
\[3:4\] done
clear
B)
\[9:16\] done
clear
C)
\[4:3\] done
clear
D)
\[\sqrt{3}:2\] done
clear
View Solution play_arrow
-
question_answer8)
If \[\Delta ABC\tilde{\ }\Delta PQR,\] perimeter of \[\Delta ABC=20cm,\] perimeter of \[\Delta PQR=40cm\] and \[\text{PR}=\text{8 cm},\]then the length of AC is:
A)
\[\text{8 cm}\] done
clear
B)
\[\text{6 cm}\] done
clear
C)
\[\text{4 cm}\] done
clear
D)
\[5\,cm\] done
clear
View Solution play_arrow
-
question_answer9)
In \[\Delta ABC,\] it is given that \[\text{AB}=\text{9cm},\]\[\text{BC}=\text{6cm}\]and \[\text{CA}=\text{7}.\text{5cm}\]. Also, \[\Delta DEF\] is given such that \[EF=8\,cm\]and\[\Delta DEF\tilde{\ }\Delta ABC\].Then, perimeter of \[\Delta DEF\] is:
A)
\[\text{22}.\text{5 cm}\] done
clear
B)
\[\text{25 cm}\] done
clear
C)
\[\text{27 cm}\] done
clear
D)
\[\text{30 cm}\] done
clear
View Solution play_arrow
-
question_answer10)
| In the given figure, if \[PQ\left\| BC \right.\]. Find AQ. |
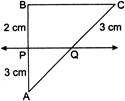 |
A)
\[\text{3}.\text{5 cm}\] done
clear
B)
\[4.\text{5 cm}\] done
clear
C)
\[\text{9 cm}\] done
clear
D)
\[\text{9}\text{.5 cm}\] done
clear
View Solution play_arrow
-
question_answer11)
If in\[\Delta ABC,\] \[AB=6cm\] and \[DE\left\| BC \right.\] such that \[AE=\frac{1}{4}AC,\]then the length of AD is:
A)
\[2\,cm\] done
clear
B)
\[1.2\,cm\] done
clear
C)
\[1.5\,cm\] done
clear
D)
\[4\,cm\] done
clear
View Solution play_arrow
-
question_answer12)
| In the adjoining figure, \[DE\left\| BC \right.\]. The value of x is: |
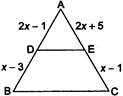 |
A)
4 done
clear
B)
6 done
clear
C)
8 done
clear
D)
10 done
clear
View Solution play_arrow
-
question_answer13)
| In figure, \[LM\left\| AB \right.\]. If \[AL=x-3,\]\[AC=2x,\]\[BM=x-2\]and \[\text{BC}=\text{2x}+\text{3},\]find the value of x. |
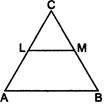 |
A)
2 done
clear
B)
\[9.5\] done
clear
C)
9 done
clear
D)
\[8.5\] done
clear
View Solution play_arrow
-
question_answer14)
| In figure, if \[\frac{AD}{DC}=\frac{BE}{EC}\] and \[\angle CDE=\angle CED,\] then: |
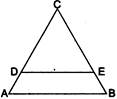 |
A)
\[\text{BC}=\text{AC}\] done
clear
B)
\[\text{AB}=\text{AC}\] done
clear
C)
\[\text{AB}=B\text{C}\] done
clear
D)
\[CE=DE\] done
clear
View Solution play_arrow
-
question_answer15)
In the given figure, DE is parallel to BC, if \[\frac{AD}{DB}=\frac{2}{3}\] and \[\text{AC}=\text{18cm},\]find AE.
A)
\[\text{6}.\text{3 cm}\] done
clear
B)
\[\text{7}\text{.2 cm}\] done
clear
C)
\[\text{6}\text{.5 cm}\] done
clear
D)
\[\text{7}\text{.6 cm}\] done
clear
View Solution play_arrow
-
question_answer16)
If \[\Delta ABC\tilde{\ }\Delta EDF\] and \[\Delta ABC\] is not similar to\[\Delta DEF,\]the which of the following is not true?
A)
\[\text{BC}.\text{EF}=\text{AC}.\text{FD}\] done
clear
B)
\[AB.\text{EF}=\text{AC}.\text{DE}\] done
clear
C)
\[\text{BC}\text{.DE}=\text{AB}.\text{EF}\] done
clear
D)
\[\text{BC}\text{.DE}=\text{AB}.\text{FD}\] done
clear
View Solution play_arrow
-
question_answer17)
It is given that \[\Delta ABC\tilde{\ }\Delta DFE,\] \[\angle A=30{}^\circ ,\] \[\angle C=50{}^\circ ,\] \[AB=5cm,\]and \[DF=7.5cm\]. Then, which of the following is true?
A)
\[DE=12cm,\,\,\,\angle F=50{}^\circ \] done
clear
B)
\[DE=12cm,\,\,\,\angle F=100{}^\circ \] done
clear
C)
\[EF=12cm,\,\,\,\angle D=100{}^\circ \] done
clear
D)
\[EF=12cm,\,\,\,\angle D=30{}^\circ \] done
clear
View Solution play_arrow
-
question_answer18)
D and E are respectively the points on the sides AB and AC of a triangle ABC such that \[\text{AD}=2\text{ cm},\] \[\text{BD}=\text{3 cm},\] \[\text{BC}=\text{7}.\text{5 cm}\]and \[DE\left\| BC \right.\].Then length of DE (in cm) is:
A)
\[2.5\] done
clear
B)
\[3\] done
clear
C)
\[5\] done
clear
D)
\[6\] done
clear
View Solution play_arrow
-
question_answer19)
Two triangles are similar if their corresponding sides are:
A)
same done
clear
B)
proportional done
clear
C)
opposite done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer20)
In \[\Delta PQR,\] S and T are points on the sides PQ and PR respectively such that \[ST\left\| QR \right.\]. If \[\text{PS}=\text{4 cm},\] \[\text{PQ}=\text{9 cm}\] and \[\text{PR}=\text{4}\text{.5cm},\]then PT is: (CBSE2014, 15, 16, 17)
A)
1 cm done
clear
B)
2 cm done
clear
C)
7 cm done
clear
D)
11cm done
clear
View Solution play_arrow
-
question_answer21)
If the corresponding medians of two similar triangles are in the ratio \[\text{5}:\text{7},\] then the ratio of their corresponding sides is: (CBSE 2015)
A)
\[\text{25}:\text{49}\] done
clear
B)
\[\text{5}:7\] done
clear
C)
\[7:5\] done
clear
D)
\[\text{49}:\text{25}\] done
clear
View Solution play_arrow
-
question_answer22)
\[\Delta ABC\tilde{\ }\Delta DEF\]. If \[AB=4cm,\] \[\text{BC}=\text{3}\text{.5 cm},\] \[\text{CA}=\text{2}\text{.5 cm}\]and \[\text{DF}=\text{7}\text{.5 cm},\]the perimeter of \[\Delta DEF\] is: (CBSE 2017)
A)
20 cm done
clear
B)
30 cm done
clear
C)
35 cm done
clear
D)
47 cm done
clear
View Solution play_arrow
-
question_answer23)
| In the given figure, value of x (in cm) is: (CBSE 2011) |
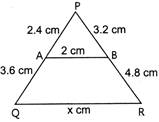 |
A)
4 done
clear
B)
5 done
clear
C)
6 done
clear
D)
8 done
clear
View Solution play_arrow
-
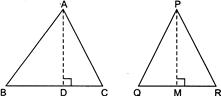
question_answer24)
| In the given figure, if\[\Delta ABC\tilde{\ }\Delta PQR\] (CBSE 2012) |
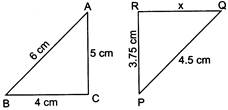 The value of x is: The value of x is: |
A)
\[\text{2}.\text{5 cm}\] done
clear
B)
\[3.\text{5 cm}\] done
clear
C)
\[\text{2}.\text{75 cm}\] done
clear
D)
\[\text{3 cm}\] done
clear
View Solution play_arrow
-
question_answer25)
"If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio." This theorem is known as:
A)
Pythagoras Theorem done
clear
B)
Laplace Theorem done
clear
C)
Thales Theorem done
clear
D)
Area Theorem done
clear
View Solution play_arrow
-
question_answer26)
"If a line divides any two sides of a triangle in the same ratio, then the Line is parallel to the third side." This theorem is known as converse of:
A)
Area Theorem done
clear
B)
Basic Proportionality Theorem done
clear
C)
Pythagoras Theorem done
clear
D)
Laplace Theorem done
clear
View Solution play_arrow
-
question_answer27)
| In the given figure, \[\frac{AD}{DB}=\frac{AE}{EC}\] and \[\angle ADE=70{}^\circ ,\]\[\angle BAC=50{}^\circ ,\]then angle \[\angle BCA=\] |
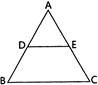 |
A)
\[70{}^\circ \] done
clear
B)
\[50{}^\circ \] done
clear
C)
\[80{}^\circ \] done
clear
D)
\[60{}^\circ \] done
clear
View Solution play_arrow
-
question_answer28)
| In the given figure, \[MN\left\| QR \right.\] and \[PM=3cm,\]\[MQ=4cm,\]\[PN=6cm,\]\[PR=x\,cm,\] then x = |
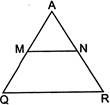 |
A)
\[8\,cm\] done
clear
B)
\[6\,cm\] done
clear
C)
\[10\,cm\] done
clear
D)
\[14\,cm\] done
clear
View Solution play_arrow
-
question_answer29)
| In the given figure, \[\text{AD}=\text{1}.\text{28 cm},\]\[\text{DB}=\text{2}\text{.56 cm},\] \[\text{AE}=0.\text{64 cm}\]. DE will be parallel to BC, if EC = |
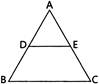 |
A)
\[\text{1}.\text{28 cm}\] done
clear
B)
\[\text{2}\text{.56 cm}\] done
clear
C)
\[0.\text{64 cm}\] done
clear
D)
\[0.\text{32 cm}\] done
clear
View Solution play_arrow
-
question_answer30)
In \[\Delta ABC\] and \[\Delta DEF,\] if \[\angle A=\angle D,\] \[\angle B=\angle E\] and \[\angle C=\angle F,\]then \[\Delta ABC\] and \[\Delta DEF\] are similar. Symbolically we write:
A)
\[\Delta ABC=\Delta DEF\] done
clear
B)
\[\Delta ABC\cong \Delta DEF\] done
clear
C)
[a] or [b] done
clear
D)
\[\Delta ABC\tilde{\ }\Delta DEF\] done
clear
View Solution play_arrow
-
question_answer31)
In \[\Delta ABC\] and \[\Delta DEF,\] \[\frac{AB}{EF}=\frac{AC}{DE},\] and \[\angle A=\angle E,\]then symbolically we write:
A)
\[\Delta ABC\tilde{\ }\Delta DEF\] done
clear
B)
\[\Delta ABC\tilde{\ }\Delta EDF\] done
clear
C)
\[\Delta ABC\tilde{\ }\Delta EFD\] done
clear
D)
\[\Delta ABC\cong \Delta EFD\] done
clear
View Solution play_arrow
-
question_answer32)
In \[\Delta PQR\]and \[\Delta MNS,\]\[\frac{PQ}{NS}=\frac{QR}{MS}=\frac{PR}{MN},\] .then symbolically we write:
A)
\[\Delta PQR\tilde{\ }\Delta MNS\] done
clear
B)
\[\Delta PQR\tilde{\ }\Delta SMP\] done
clear
C)
\[\Delta QRP\tilde{\ }\Delta NSN\] done
clear
D)
\[\Delta QRP\tilde{\ }\Delta SMN\] done
clear
View Solution play_arrow
-
question_answer33)
The parallel sides of a trapezoid are \[3\,cm\] and \[9\,cm\]. The non-parallel sides are \[4\,cm\] and \[6\,cm\]. A line parallel to the base divides the trapezoid into two trapezoids of equal perimeters. The ratio in which each of the non-parallel sides is divided, is:
A)
\[4:5\] done
clear
B)
\[3:2\] done
clear
C)
\[4:1\] done
clear
D)
\[3:1\] done
clear
View Solution play_arrow
-
question_answer34)
In the given figure, ABC is a triangle and CHED is a rectangle. \[BC=12cm,\] \[HF=6cm,\] \[\text{FC}=\text{BF}\]and altitude AF is 24 cm. The area of rectangle is:
A)
\[56c{{m}^{2}}\] done
clear
B)
\[54c{{m}^{2}}\] done
clear
C)
\[60c{{m}^{2}}\] done
clear
D)
\[72c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer35)
| In given figure \[AD=3cm,\] \[AE=5cm,\] \[BD=4cm,\] \[CE=4cm,\] \[CF=2cm,\] \[BF=2.5cm,\] then: |
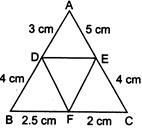 |
A)
\[DE\left\| BC \right.\] done
clear
B)
\[DF\left\| AC \right.\] done
clear
C)
\[EF\left\| AB \right.\] done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer36)
| The value of x in the given figure: |
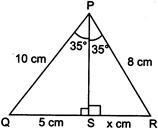 |
A)
\[5\,cm\] done
clear
B)
\[4\,cm\] done
clear
C)
\[2\,cm\] done
clear
D)
\[3\,cm\] done
clear
View Solution play_arrow
-
question_answer37)
| In the given figure,\[DE\left\| BC \right.\]. The value of EC is: |
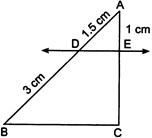 |
A)
1.5 cm done
clear
B)
3 cm done
clear
C)
2 cm done
clear
D)
1 cm done
clear
View Solution play_arrow
-
question_answer38)
It is given that, \[\Delta ABC\tilde{\ }\Delta EDF\]such that \[\text{AB}=\text{5 cm},\] \[\text{AC}=\text{7 cm},\] \[\text{DF}=\text{15 cm}\] and \[\text{DE}=\text{12 cm},\]then the sum of the remaining sides of the triangles is:
A)
\[\text{23}.0\text{5 cm}\] done
clear
B)
\[\text{16}.\text{8 cm}\] done
clear
C)
\[\text{6}.\text{25 cm}\] done
clear
D)
\[\text{24 cm}\] done
clear
View Solution play_arrow
-
question_answer39)
If in two triangles, corresponding sides are in the same ratio, then the two triangles are similar. This criterion is known as:
A)
SSS similarity criterion done
clear
B)
SAS similarity criterion done
clear
C)
AA similarity criterion done
clear
D)
AAA similarity criterion done
clear
View Solution play_arrow
-
question_answer40)
If in two similar triangles ABC and DEF, \[\frac{AB}{DE}=\frac{BC}{EF},\] then:
A)
\[\angle B=\angle E\] done
clear
B)
\[\angle A=\angle E\] done
clear
C)
\[\angle B=\angle D\] done
clear
D)
\[\angle A=\angle F\] done
clear
View Solution play_arrow
-
question_answer41)
In two triangles ABC and DEF, \[\angle A=\angle E\] and \[\angle B=\angle F\]. Then, \[\frac{AB}{AC}\] is equal to:
A)
\[\frac{DE}{DF}\] done
clear
B)
\[\frac{ED}{EF}\] done
clear
C)
\[\frac{EF}{ED}\] done
clear
D)
\[\frac{EF}{DF}\] done
clear
View Solution play_arrow
-
question_answer42)
| In the given figure, \[\angle BAC=90{}^\circ \] and \[AD\bot BC,\] then: |
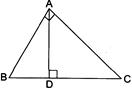 |
A)
\[BD\times CD=B{{C}^{2}}\] done
clear
B)
\[AB\times AC=B{{C}^{2}}\] done
clear
C)
\[BD\times CD=A{{D}^{2}}\] done
clear
D)
\[AB\times AC=A{{D}^{2}}\] done
clear
View Solution play_arrow
-
question_answer43)
| In the given figure, if \[AB\left\| DC \right.,\] find the value of x. |
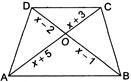 |
A)
5 done
clear
B)
7 done
clear
C)
6 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer44)
| In the figure, find x in terms of a, b and c. |
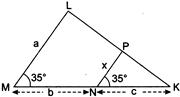 |
A)
\[\frac{ab}{a+c}\] done
clear
B)
\[\frac{ac}{b+c}\] done
clear
C)
\[\frac{bc}{a+b}\] done
clear
D)
\[\frac{ac}{a+b}\] done
clear
View Solution play_arrow
-
question_answer45)
\[\Delta ABC\] is a right triangle, right-angled at A and \[AD\bot BC\]. Then, \[\frac{BD}{DC}\] is equal to:
A)
\[{{\left( \frac{AB}{AC} \right)}^{2}}\] done
clear
B)
\[\frac{AB}{AC}\] done
clear
C)
\[{{\left( \frac{AB}{AD} \right)}^{2}}\] done
clear
D)
\[\frac{AB}{AD}\] done
clear
View Solution play_arrow
-
question_answer46)
\[ABCD\] is a trapezium such that \[\left. BC \right\|AD\] and \[\text{AB}=\text{4cm}\]. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC}=\frac{OB}{OD}=\frac{1}{2},\]then CD=
A)
7 cm done
clear
B)
8 cm done
clear
C)
9 cm done
clear
D)
6 cm done
clear
View Solution play_arrow
-
question_answer47)
A vertical stick 12m long casts a shadow 8m long on the ground. At the same time a tower casts the shadow 40m long on the ground. Then the height of the tower is:
A)
65 m done
clear
B)
60 m done
clear
C)
70 m done
clear
D)
72 m done
clear
View Solution play_arrow
-
question_answer48)
| In the figure, if \[\angle BAC=90{}^\circ \] and \[AD\bot BC,\] then: (NCERT EXEMPLAR) |
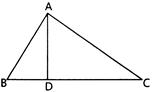 |
A)
\[BD.CD=B{{C}^{2}}\] done
clear
B)
\[AB.AC=B{{C}^{2}}\] done
clear
C)
\[BD.CD=A{{D}^{2}}\] done
clear
D)
\[AB.AC=A{{D}^{2}}\] done
clear
View Solution play_arrow
-
question_answer49)
If in two triangles ABC and PQR, \[\frac{AB}{QR}=\frac{BC}{PR}=\frac{CA}{PQ},\] then: (NCERT EXEMPLAR)
A)
\[\Delta PQR\tilde{\ }\Delta CAB\] done
clear
B)
\[\Delta PQR\tilde{\ }\Delta ABC\] done
clear
C)
\[\Delta CBA\tilde{\ }\Delta PQR\] done
clear
D)
\[\Delta BCA\tilde{\ }\Delta PQR\] done
clear
View Solution play_arrow
-
question_answer50)
If in two triangles DEF and PQR, \[\angle D=\angle Q\] and then which of the following is not true? (NCERT EXEMPLAR)
A)
\[\frac{EF}{PR}=\frac{DF}{PQ}\] done
clear
B)
\[\frac{DE}{PQ}=\frac{EF}{RP}\] done
clear
C)
\[\frac{DE}{QR}=\frac{DF}{PQ}\] done
clear
D)
\[\frac{EF}{RP}=\frac{DE}{QR}\] done
clear
View Solution play_arrow
-
question_answer51)
In triangles ABC and DEF, \[\angle B=\angle E,\] \[\angle F=\angle C\] and \[AB=3DE.\]Then, the two triangles are: (NCERT EXEMPLAR)
A)
congruent but not similar done
clear
B)
similar but not congruent done
clear
C)
neither congruent nor similar done
clear
D)
congruent as well as similar. done
clear
View Solution play_arrow
-
question_answer52)
If in triangles ABC and DEF, \[\frac{AB}{DE}=\frac{BC}{FD},\] then they will be similar, when: (NCERT EXEMPLAR)
A)
\[\angle B=\angle E\] done
clear
B)
\[\angle A=\angle D\] done
clear
C)
\[\angle B=\angle D\] done
clear
D)
\[\angle A=\angle F\] done
clear
View Solution play_arrow
-
question_answer53)
| If in fig., O is the point of intersection of two chords AB and CD such that \[\text{OB}=\text{OD},\]then triangles OAC and ODB are: (NCERT EXEMPLAR) |
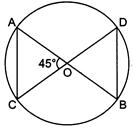 |
A)
equilateral but not similar done
clear
B)
isosceles but not similar done
clear
C)
equilateral and similar done
clear
D)
isosceles and similar done
clear
View Solution play_arrow
-
question_answer54)
| In the given figure, if \[DE\left\| BC, \right.\] \[\text{AE}=\text{8}\,\text{cm},\] \[\text{EC}=\text{2 cm}\] and \[\text{BC}=\text{6 cm},\]then DE is: (CBSE 2014) |
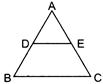 |
A)
\[\text{2}.\text{7 cm}\] done
clear
B)
\[3.2\text{ cm}\] done
clear
C)
\[4.4\text{ cm}\] done
clear
D)
\[4.8\text{ cm}\] done
clear
View Solution play_arrow
-
question_answer55)
If PQR is an equilateral triangle and \[PX\bot QR,\] then \[P{{X}^{2}}\] is equal to: (CBSE 2013)
A)
\[{{(RX)}^{2}}\] done
clear
B)
\[2{{(RX)}^{2}}\] done
clear
C)
\[3{{(RX)}^{2}}\] done
clear
D)
\[2RX\] done
clear
View Solution play_arrow
-
question_answer56)
In a \[\Delta PQR,\] S and T are points on the sides PQ and PR respectively, such that \[ST\left\| QR \right.\]. If \[\text{PT}=2\text{cm}\] and \[\text{TR}=\text{4cm},\]then the ratio of the areas of \[\Delta PST\] and \[\Delta PQR\] is:
A)
\[1:9\] done
clear
B)
\[1:3\] done
clear
C)
\[1:2\] done
clear
D)
\[1:4\] done
clear
View Solution play_arrow
-
question_answer57)
If in two right triangles, hypotenuse and one side of one triangle are proportional to the hypotenuse and one side of the other triangle, then the two triangles are similar. This may be referred to as the:
A)
AAA similarity criterion done
clear
B)
ASS similarity criterion done
clear
C)
SAS similarity criterion done
clear
D)
RHS similar criterion done
clear
View Solution play_arrow
-
question_answer58)
| In the given figure, express x in terms of a, b and c. |
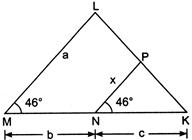 |
A)
\[x=\frac{ab}{a+b}\] done
clear
B)
\[x=\frac{ac}{b+c}\] done
clear
C)
\[x=\frac{bc}{b+c}\] done
clear
D)
\[x=\frac{ac}{a+c}\] done
clear
View Solution play_arrow
-
question_answer59)
Which of the following statement is false?
A)
All isosceles triangles are similar. done
clear
B)
All quadrilateral triangles are similar. done
clear
C)
All circles are similar. done
clear
D)
None of the above. done
clear
View Solution play_arrow
-
question_answer60)
If the ratio of the perimeters of two similar triangles is \[\text{4}:\text{25},\]then the ratio of the areas of the similar triangles is:
A)
\[\text{16}:\text{625}\] done
clear
B)
\[\text{2}:\text{5}\] done
clear
C)
\[5:2\] done
clear
D)
\[\text{625}:\text{16}\] done
clear
View Solution play_arrow
-
question_answer61)
Ratio of areas of two similar triangles is\[\text{2}:\text{3}\]. Then ratio of their corresponding sides is:
A)
\[\sqrt{3}:\sqrt{2}\] done
clear
B)
\[\sqrt{6}:1\] done
clear
C)
\[1:\sqrt{6}\] done
clear
D)
\[\sqrt{2}:\sqrt{3}\] done
clear
View Solution play_arrow
-
question_answer62)
The areas of two similar triangles are \[25c{{m}^{2}}\]and \[36c{{m}^{2}}\].If the median of the smaller triangle is \[\text{1}0\text{ cm},\] then the median of the larger triangle is:
A)
\[12cm\] done
clear
B)
\[15cm\] done
clear
C)
\[10cm\] done
clear
D)
\[18cm\] done
clear
View Solution play_arrow
-
question_answer63)
Two isosceles triangles have equal angles and their areas are in the ratio\[\text{16}:\text{25}\]. The ratio of their corresponding altitudes is:
A)
4:5 done
clear
B)
5:4 done
clear
C)
3:2 done
clear
D)
5:7 done
clear
View Solution play_arrow
-
question_answer64)
\[\Delta ABC\tilde{\ }\Delta PQR\] such that \[ar(\Delta ABC)=4ar(\Delta PQR)\]. If \[BC=12\,cm,\]then \[QR=\]
A)
9 cm done
clear
B)
10 cm done
clear
C)
6 cm done
clear
D)
8 cm done
clear
View Solution play_arrow
-
question_answer65)
In a trapezium \[ABCD,\]\[\left. AB \right\|CD\] and its diagonals intersect at O. If \[\text{AB}=\text{6 cm}\] and \[\text{DC}=\text{3 cm},\]then find the ratio of the areas of \[\Delta AOB\] and \[\Delta COD\].
A)
4:1 done
clear
B)
1:2 done
clear
C)
2:1 done
clear
D)
1:4 done
clear
View Solution play_arrow
-
question_answer66)
In a \[\Delta ABC,\] \[\left. DE \right\|BC.\]If \[DE=\frac{3}{2}BC\] and area of \[\Delta ABC=81c{{m}^{2}}\] then the area of \[\Delta ADE\]is:
A)
\[\text{25 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{36 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{6 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{5 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer67)
If D,E,F are the mid-points of sides BC,CA and AB respectively of MBC, then the ratio of the areas of triangles DEF and ABC is:
A)
1:4 done
clear
B)
1:2 done
clear
C)
2:3 done
clear
D)
4:5 done
clear
View Solution play_arrow
-
question_answer68)
ABC and BDE are two equilateral triangles such that D is the mid-point of SC. Ratio of the areas of triangles ABC and BDE is:
A)
2:1 done
clear
B)
1:2 done
clear
C)
4:1 done
clear
D)
1:4 done
clear
View Solution play_arrow
-
question_answer69)
It is given that \[\Delta ABC\tilde{\ }\Delta PQR\]with \[\frac{BC}{QR}=\frac{1}{3}.\] Then \[\frac{ar\,(\Delta PQR)}{ar(\Delta ABC)}\] is equal to: (NCERT EXEMPLAR)
A)
\[9\] done
clear
B)
\[3\] done
clear
C)
\[\frac{1}{3}\] done
clear
D)
\[\frac{1}{9}\] done
clear
View Solution play_arrow
-
question_answer70)
If \[\Delta ABC\tilde{\ }\Delta QRP,\] \[\frac{ar(ABC)}{ar(PQR)}=\frac{9}{4},\] \[AB=18\,cm\] and \[BC=15\,cm,\] then PR is equal to: (NCERT EXEMPLAR)
A)
\[10\,cm\] done
clear
B)
\[12\,cm\] done
clear
C)
\[\frac{20}{3}\,cm\] done
clear
D)
\[8\,cm\] done
clear
View Solution play_arrow
-
question_answer71)
| In the given figure, \[\Delta ABC\tilde{\ }\Delta PQR\]. If \[\text{BC}=\text{5 cm}\] and \[\text{QR}=\text{3cm},\]then the ratio of areas of \[\Delta ABC\]to \[\Delta PQR\] is: |
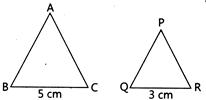 |
A)
\[5:3\] done
clear
B)
\[3:5\] done
clear
C)
\[25:9\] done
clear
D)
\[9:25\] done
clear
View Solution play_arrow
-
question_answer72)
| In the given figure, \[\Delta MNP\tilde{\ }\Delta ABC\] such that \[\text{MN}=\text{6 cm},\] \[\text{AB}=8\,\text{cm}\] and area of \[\Delta MNP\] is \[\text{15 c}{{\text{m}}^{\text{2}}},\] then the area of \[\Delta ABC\] is: |
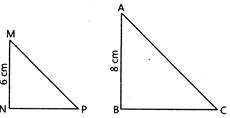 |
A)
\[26.66c{{m}^{2}}\] done
clear
B)
\[16.66c{{m}^{2}}\] done
clear
C)
\[20\,c{{m}^{2}}\] done
clear
D)
\[None\,\, of\,\, these\] done
clear
View Solution play_arrow
-
question_answer73)
| In \[\Delta ABC,\] \[\left. DE \right\|BC.\] If \[DE=4cm,\] \[BC=8cm\]and area of \[\Delta ADE=25c{{m}^{2}},\]then the area of \[\Delta ABC\]is: |
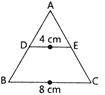 |
A)
\[50\,c{{m}^{2}}\] done
clear
B)
\[100\,c{{m}^{2}}\] done
clear
C)
\[75\,c{{m}^{2}}\] done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer74)
The ratio of the areas of two similar triangles is equal to the............... of the ratio of their corresponding sides.
A)
square done
clear
B)
cube done
clear
C)
twice done
clear
D)
thrice done
clear
View Solution play_arrow
-
question_answer75)
| In fig. \[\left. MN \right\|BC\] and \[\text{AM}:\text{MB}=\text{1}:\text{2},\]then \[\frac{ar(\Delta AMN)}{ar(\Delta ABC)}\] is: |
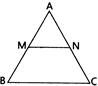 |
A)
\[1:4\] done
clear
B)
\[1:9\] done
clear
C)
\[1:1\] done
clear
D)
\[1:2\] done
clear
View Solution play_arrow
-
question_answer76)
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is: (NCERT EXERCISE)
A)
\[2:1\] done
clear
B)
\[1:2\] done
clear
C)
\[4:1\] done
clear
D)
\[1:4\] done
clear
View Solution play_arrow
-
question_answer77)
Sides of two similar triangles are in the ratio\[\text{3}:\text{4}\]. Areas of these triangles are in the ratio: (NCERT EXERCISE)
A)
\[2:3\] done
clear
B)
\[4:9\] done
clear
C)
\[81:16\] done
clear
D)
\[9:16\] done
clear
View Solution play_arrow
-
question_answer78)
Given \[\Delta ABC\tilde{\ }PQR,\]if \[\frac{AB}{PQ}=\frac{1}{3},\]then \[\frac{ar(\Delta ABC)}{ar(\Delta PQR)}\]is:
A)
\[1:3\] done
clear
B)
\[3:1\] done
clear
C)
\[9:1\] done
clear
D)
\[1:9\] done
clear
View Solution play_arrow
-
question_answer79)
| In figure, \[\left. DE \right\|BC,\] \[\text{AD}=\text{1 cm}\] and \[\text{BD}=\text{2 cm}\]. The ratio of the \[ar(\Delta ABC)\]to the \[ar(\Delta ADE)\] is : |
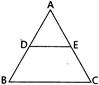 |
A)
\[1:9\] done
clear
B)
\[9:1\] done
clear
C)
\[1:2\] done
clear
D)
\[1:4\] done
clear
View Solution play_arrow
-
question_answer80)
| The area of two similar triangles are \[\text{25 c}{{\text{m}}^{\text{2}}}\] and\[\text{121 c}{{\text{m}}^{\text{2}}}\]. |
| The ratio of their sides is: (CBSE 2019) |
A)
\[\text{25}:\text{121}\] done
clear
B)
\[\text{5}:\text{11}\] done
clear
C)
\[121:25\] done
clear
D)
\[11:5\] done
clear
View Solution play_arrow
-
question_answer81)
Two similar triangles ABC and PQR have their areas \[25c{{m}^{2}}\] and \[49c{{m}^{2}}\] respectively. If \[QR=9.8cm,\]the value of BC is: (CBSE 2020)
A)
7 cm done
clear
B)
4 cm done
clear
C)
8 cm done
clear
D)
9 cm done
clear
View Solution play_arrow
-
question_answer82)
Sides of two similar triangles are in the ratio \[3:7.\] Areas of these triangles are in the ratio:
A)
\[9:35\] done
clear
B)
\[9:49\] done
clear
C)
\[49:9\] done
clear
D)
\[9:42\] done
clear
View Solution play_arrow
-
question_answer83)
| In right triangles \[ABC,\] \[BC=a,\] \[AC=b,\]\[AB=c,\] \[CD\bot AB.\] If area of \[\Delta ABC=A,\] then \[CD=\] |
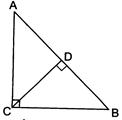 |
A)
\[\frac{2A}{C}\] done
clear
B)
\[\frac{A}{C}\] done
clear
C)
\[\frac{A}{2C}\] done
clear
D)
\[\frac{C}{A}\] done
clear
View Solution play_arrow
-
question_answer84)
| In the given figure, ABC is an equilateral triangles DE is parallel to BC such that area of quadrilateral DBCE is equal to one half the area of \[\Delta ABC\]. If \[BC=2cm,\] then \[DE=\] |
 |
A)
\[1cm\] done
clear
B)
\[1\frac{1}{2}cm\] done
clear
C)
\[\sqrt{2}cm\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer85)
| If \[\Delta ABC\tilde{\ }\Delta PQR,\] area of \[\Delta ABC=81c{{m}^{2}}\] and area of \[\Delta PQR=121c{{m}^{2}}\] and altitude \[\text{AD}=\text{9 cm},\]then \[PM=\] |
 |
A)
10 cm done
clear
B)
11 cm done
clear
C)
12 cm done
clear
D)
15 cm done
clear
View Solution play_arrow
-
question_answer86)
| In the given figure, P and Q are points on the sides AB and AC respectively of a triangle ABC. PQ is parallel to BC and divides the triangle ABC into two parts, equal in area. The ratio of \[\text{PA}:\text{AB}=\] |
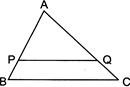 |
A)
\[1:1\] done
clear
B)
\[(\sqrt{2}-1):\sqrt{2}\] done
clear
C)
\[1:\sqrt{2}\] done
clear
D)
\[(\sqrt{2}-1):1\] done
clear
View Solution play_arrow
-
question_answer87)
If \[\Delta ABC\tilde{\ }\Delta APQ\] and \[ar(\Delta APQ)=4ar(\Delta ABC),\] then the ratio of \[BC\]to \[PQ\] is:
A)
\[2:1\] done
clear
B)
\[1:2\] done
clear
C)
\[1:4\] done
clear
D)
\[4:1\] done
clear
View Solution play_arrow
-
question_answer88)
The areas of two similar triangles are \[\text{81 c}{{\text{m}}^{\text{2}}}\] and \[\text{49 c}{{\text{m}}^{\text{2}}}\]respectively, then the ratio of their corresponding medians is:
A)
\[7:9\] done
clear
B)
\[9:81\] done
clear
C)
\[9:7\] done
clear
D)
\[81:7\] done
clear
View Solution play_arrow
-
question_answer89)
Sides of two similar triangles are in the ratio \[\text{4}:\text{9}\]. Areas of these triangles are in the ratio:
A)
\[2:3\] done
clear
B)
\[4:9\] done
clear
C)
\[81:16\] done
clear
D)
\[16:81\] done
clear
View Solution play_arrow
-
question_answer90)
In an isosceles triangle \[ABC,\] if \[\text{AC}=\text{BC}\] and \[\text{A}{{\text{B}}^{\text{2}}}=\text{2A}{{\text{C}}^{\text{2}}}\]then \[\angle C\] is equal to:
A)
\[30{}^\circ \] done
clear
B)
\[45{}^\circ \] done
clear
C)
\[90{}^\circ \] done
clear
D)
\[60{}^\circ \] done
clear
View Solution play_arrow
-
question_answer91)
\[\Delta ABC\]is an isosceles triangle in which \[\angle C=90{}^\circ \]. If \[\text{BC}=\text{4cm},\]then find AB.
A)
\[4\sqrt{2}\,cm\] done
clear
B)
\[2\sqrt{2}\,cm\] done
clear
C)
\[4\,cm\] done
clear
D)
\[2\,cm\] done
clear
View Solution play_arrow
-
question_answer92)
| Two poles of height \[13\,m\] and \[7\,m\] respectively stand vertically on a plane ground at a distance of \[8\,m\] from each other. The distance between their tops is: |
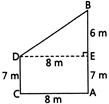 |
A)
\[9\,m\] done
clear
B)
\[10\,m\] done
clear
C)
\[11\,m\] done
clear
D)
\[12\,m\] done
clear
View Solution play_arrow
-
question_answer93)
The lengths of the diagonals of a rhombus are \[24\,m\] and \[10\,m\]. The length of each side of the rhombus is:
A)
\[12cm\] done
clear
B)
\[13cm\] done
clear
C)
\[14cm\] done
clear
D)
\[17cm\] done
clear
View Solution play_arrow
-
question_answer94)
The length of the diagonal of a square is \[7\sqrt{2}cm.\]. Then, the area of the square (in \[\text{c}{{\text{m}}^{\text{2}}}\]) is:
A)
\[28\] done
clear
B)
\[14\sqrt{2}\] done
clear
C)
\[21\] done
clear
D)
\[49\] done
clear
View Solution play_arrow
-
question_answer95)
An aeroplane leaves an airport and flies due North at a speed of \[300\,km\] per hour. At the same time, another aeroplane leaves the same airport and flies due West at a speed of \[500\,km\] per hour. How far apart will be two planes after \[1\frac{1}{2}\] hours?
A)
\[200\sqrt{29}\,km\] done
clear
B)
\[100\sqrt{3}\,km\] done
clear
C)
\[150\sqrt{34}\,km\] done
clear
D)
\[250\sqrt{34}\,km\] done
clear
View Solution play_arrow
-
question_answer96)
| ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB respectively. Then the ratio between the areas of\[\Delta ABE\] and \[\Delta ACD\] is: |
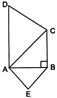 |
A)
\[2:1\] done
clear
B)
\[1:2\] done
clear
C)
\[1:3\] done
clear
D)
\[3:1\] done
clear
View Solution play_arrow
-
question_answer97)
The lengths of the diagonals of a rhombus are \[\text{16}\,\text{cm}\] and \[\text{12}\,\text{cm}\]. Then, the length of the side of the rhombus is: (NCERT EXEMPLAR)
A)
\[9\,\text{cm}\] done
clear
B)
\[10\,\text{cm}\] done
clear
C)
\[8\,\text{cm}\] done
clear
D)
\[20\,\text{cm}\] done
clear
View Solution play_arrow
-
question_answer98)
A ladder \[\text{1}0\,\text{m}\] long reaches a window \[8\,\text{m}\] above the ground. The distance of the foot of the ladder from the base of the wall is: (NCERT EXERCISE)
A)
2 m done
clear
B)
18 m done
clear
C)
6 m done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer99)
A man goes \[18\,\text{m}\] due East and then \[24\,\text{m}\] due North. He is away from the starting point by:
A)
\[30\,\text{m}\] done
clear
B)
\[20\,\text{m}\] done
clear
C)
\[24\,\text{m}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer100)
In \[\Delta ABC,\] \[AB=6\sqrt{3}cm,\] \[AC=12cm\]and \[\text{BC}=\text{6 cm}\]. The angle B is: (NCERT EXERCISE; CBSE 2020)
A)
\[120{}^\circ \] done
clear
B)
\[60{}^\circ \] done
clear
C)
\[90{}^\circ \] done
clear
D)
\[45{}^\circ \] done
clear
View Solution play_arrow
-
question_answer101)
A girl walks \[\text{5}00\,\text{m}\] towards East and then \[1200\,\text{m}\] towards North. Find her distance from the starting point (cbse 2016)
A)
\[1100\,\text{m}\] done
clear
B)
\[1200\,\text{m}\] done
clear
C)
\[1300\,\text{m}\] done
clear
D)
\[1400\,\text{m}\] done
clear
View Solution play_arrow
-
question_answer102)
A ladder \[\text{25}\,\text{m}\] long just reaches the top of a building \[\text{24}\,\text{m}\]high from the ground. What is the distance of the foot of ladder from the base of the building? (CBSE 2020)
A)
5 m done
clear
B)
6 m done
clear
C)
7 m done
clear
D)
8 m done
clear
View Solution play_arrow
-
question_answer103)
| Sides of triangles are |
| (i) \[\text{3 cm},\text{ 4 cm},\text{ 6 cm}.\] |
| (ii) \[\text{4 cm},\text{ 5 cm},\text{ 6 cm}.\] |
| (iii) \[\text{7 cm},\text{ 24 cm},\text{ 25 cm}.\] |
| (iv) \[\text{5 cm},\text{ 12 cm},\text{ 14 cm}.\] |
| Which of these is a right triangle? |
A)
(i) done
clear
B)
(ii) done
clear
C)
(iii) done
clear
D)
(iv) done
clear
View Solution play_arrow
-
question_answer104)
The medians of a right triangle which are drawn from the vertices of the acute angles are \[\text{5 cm}\] and \[\text{2}\sqrt{10}\text{ cm}\]. The hypotenuse of the triangle is:
A)
\[\text{10 cm}\] done
clear
B)
\[\text{2}\sqrt{40}\text{ cm}\] done
clear
C)
\[\sqrt{13}\text{ cm}\] done
clear
D)
\[2\sqrt{13}\text{ cm}\] done
clear
View Solution play_arrow
-
question_answer105)
The sides of a triangle are 30, 70 and 80 units. If an altitude is droped upon the side of length 80 units, the larger segment cut off on this side is:
A)
62 units done
clear
B)
63 units done
clear
C)
64 units done
clear
D)
65 units done
clear
View Solution play_arrow
-
question_answer106)
Match the column:
| 1. | The ratio of any two corresponding sides in equiangulaqr triangles is always the same | [a] | Baudhayana |
| 2. | The diagonal of a rectangle produces by itself the same area as produced by its both sides (i. e., length and breadth) | [b] | Thales |
| 3. | In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. | [c] | Pythagoras |
| | | [d] | Aryabhatta |
A)
1\[\to \]A, 2\[\to \]B, 3\[\to \]C done
clear
B)
1\[\to \]B, 2\[\to \]A, 3\[\to \]C done
clear
C)
1\[\to \]B, 2\[\to \]C, 3\[\to \]A done
clear
D)
1\[\to \]B, 2\[\to \]A, 3\[\to \]D done
clear
View Solution play_arrow
-
question_answer107)
In \[\Delta ABC,\] \[AB=6\sqrt{3}cm,\] \[AC=12cm,\] and \[\text{BC}=\text{6 cm}\]. The angle B is:
A)
\[120{}^\circ \] done
clear
B)
\[60{}^\circ \] done
clear
C)
\[90{}^\circ \] done
clear
D)
\[45{}^\circ \] done
clear
View Solution play_arrow
-
question_answer108)
The area of a right angled isosceles triangle whose hypotenuse is equal to \[\text{27}0\,\text{m}\] is:
A)
\[\text{19}000\text{ }{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{18225 }{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{17256 }{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{18325 }{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer109)
The length of the side of a square whose diagonal is \[\text{16 cm},\] is:
A)
\[\text{8}\sqrt{2}\text{ cm}\] done
clear
B)
\[2\sqrt{8}\text{ cm}\] done
clear
C)
\[4\sqrt{2}\text{ cm}\] done
clear
D)
\[2\sqrt{2}\text{ cm}\] done
clear
View Solution play_arrow
-
question_answer110)
\[\Delta ABC\] is an equilateral triangle with each side of length \[\text{2p}\]. If \[AD\bot BC\] the then value of AD is:
A)
\[\sqrt{3}\] done
clear
B)
\[\sqrt{3}p\] done
clear
C)
\[2p\] done
clear
D)
\[4p\] done
clear
View Solution play_arrow
-
question_answer111)
In a right angled \[\Delta ABC\] right angled at B, if P and Q are points on the sides AB and BC respectively, then:
A)
\[A{{Q}^{2}}+C{{P}^{2}}=2{{(A{{C}^{2}}+PQ)}^{2}}\] done
clear
B)
\[2(A{{Q}^{2}}+C{{P}^{2}})=A{{C}^{2}}+P{{Q}^{2}}\] done
clear
C)
\[A{{Q}^{2}}+C{{P}^{2}}=A{{C}^{2}}+P{{Q}^{2}}\] done
clear
D)
\[AQ+CP=\frac{1}{2}(AC+PQ)\] done
clear
View Solution play_arrow
-
question_answer112)
The area of a right angled triangle is \[\text{4}0\text{ sq cm}\] and its perimeter is \[\text{4}0\text{ cm}\]. The length of its hypotenuse is:
A)
\[\text{16 cm}\] done
clear
B)
\[\text{18 cm}\] done
clear
C)
\[\text{17 cm}\] done
clear
D)
data insufficient. done
clear
View Solution play_arrow
-
question_answer113)
| In the figure given below, \[\angle ABC=90{}^\circ ,\] \[AD=15cm\]and \[DC=20cm\]. If BD is the bisector of \[\angle ABC,\] What is the perimeter of the triangle ABC? |
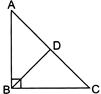 |
A)
\[74\,cm\] done
clear
B)
\[84\,cm\] done
clear
C)
\[91\,cm\] done
clear
D)
\[105\,cm\] done
clear
View Solution play_arrow
-
question_answer114)
A \[\text{5 m}\] Long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point \[\text{4 m}\] height If the foot of the ladder is moved \[\text{1}\text{.6 m}\] towards the wall, then the distance by which the top of the ladder would slide upwards on the wall is:
A)
\[\text{0}\text{.6 m}\] done
clear
B)
\[\text{0}\text{.2 m}\] done
clear
C)
\[\text{0}\text{.4 m}\] done
clear
D)
\[\text{0}\text{.8 m}\] done
clear
View Solution play_arrow
-
question_answer115)
Match the column:
| 1. | In \[\Delta ABC\] and \[\Delta PQR\] \[\frac{AB}{PQ}=\frac{AC}{PR},\]\[\angle A=\angle P\] \[\Rightarrow \,\,\Delta ABC\tilde{\ }\Delta PQR\] | [a] | AA similarity criterion |
| 2. | In \[\Delta ABC\] and \[\Delta PQR\] \[\angle A=\angle P,\] \[\angle B=\angle Q\] \[\Rightarrow \,\,\Delta ABC\tilde{\ }\Delta PQR\] | [b] | SAS similarity criterion |
| 3. | In \[\Delta ABC\] and \[\Delta PQR\] \[\frac{AB}{PQ}=\frac{AC}{PR}=\frac{BC}{QR}\] \[\Rightarrow \,\,\Delta ABC\tilde{\ }\Delta PQR\] | [c] | SSS similarity criterion |
| 4. | In \[\Delta ABC,\] \[\left. DE \right\|BC\] \[\Rightarrow \,\,\frac{AD}{BD}=\frac{AE}{CE}\] | [d] | BPT |
A)
1\[\to \]A, 2\[\to \]B, 3\[\to \]C, 4\[\to \]D done
clear
B)
1\[\to \]D, 2\[\to \]A, 3\[\to \]C, 4\[\to \]B done
clear
C)
1\[\to \]B, 2\[\to \]A, 3\[\to \]C, 4\[\to \]D done
clear
D)
1\[\to \]C, 2\[\to \]B, 3\[\to \]D, 4\[\to \]A done
clear
View Solution play_arrow










