-
question_answer1)
If the sum of the areas of two circles with radii \[{{R}_{1}}\] and \[{{R}_{2}}\] is equal to the area of a circle of radius R, then: (NCERT EXEMPLAR)
A)
\[{{R}_{1}}+{{R}_{2}}=R\] done
clear
B)
\[R_{1}^{2}+R_{2}^{2}={{R}^{2}}\] done
clear
C)
\[{{R}_{1}}+{{R}_{2}}<R\] done
clear
D)
\[R_{1}^{2}+R_{2}^{2}<{{R}^{2}}\] done
clear
View Solution play_arrow
-
question_answer2)
If the sum of the circumferences of two circles with radii \[{{R}_{1}}\]and \[{{R}_{2}}\] is equal to the circumference of a circle of radius R, then: (NCERT EXEMPLAR)
A)
\[{{R}_{1}}+{{R}_{2}}=R\] done
clear
B)
\[{{R}_{1}}+{{R}_{2}}>R\] done
clear
C)
\[{{R}_{1}}+{{R}_{2}}<R\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer3)
If the perimeter of a circle is equal to that of a square, then the ratio of their areas is: (NCERT exemplar)
A)
\[22:7\] done
clear
B)
\[14:11\] done
clear
C)
\[7:22\] done
clear
D)
\[11:14\] done
clear
View Solution play_arrow
-
question_answer4)
If the area of a circle is \[\text{154 c}{{\text{m}}^{\text{2}}},\]then its perimeter is: (NCERT EXEMPLAR)
A)
\[11\,cm\] done
clear
B)
\[22\,cm\] done
clear
C)
\[44\,cm\] done
clear
D)
\[55\,cm\] done
clear
View Solution play_arrow
-
question_answer5)
Distance moved or covered by a wheel in 1 rotation is equal to ......... of the wheel.
A)
diameter done
clear
B)
circumference done
clear
C)
area done
clear
D)
radius done
clear
View Solution play_arrow
-
question_answer6)
The area of a road which is 7 m wide and that surrounds a circular park whose circumference is \[\text{352 m}\] is ..........
A)
\[2310\,{{m}^{2}}\] done
clear
B)
\[1513\,{{m}^{2}}\] done
clear
C)
\[1920\,{{m}^{2}}\] done
clear
D)
\[2854\,{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer7)
The perimeter of a semicircle whose radius is \[\text{7 cm},\] is:
A)
\[\text{18 cm}\] done
clear
B)
\[\text{26 cm}\] done
clear
C)
\[\text{30 cm}\] done
clear
D)
\[\text{36}\,\text{cm}\] done
clear
View Solution play_arrow
-
question_answer8)
The area of a circular play ground is\[\text{22176 c}{{\text{m}}^{2}}\]. Find the cost of fencing this ground at the rate of Rs. 50 per metre.(NCERT EXEMPLAR; CBSE2020)
A)
Rs. 650 done
clear
B)
Rs. 355 done
clear
C)
Rs. 460 done
clear
D)
Rs. 264 done
clear
View Solution play_arrow
-
question_answer9)
The radii of two circles are \[4\,cm\]and \[3\,cm\]respectively. The diameter of the circle having area equal to the sum of the areas of the two circles (in cm) is: (NCERT EXEMPLAR; CBSE 2020)
A)
5 done
clear
B)
7 done
clear
C)
10 done
clear
D)
14 done
clear
View Solution play_arrow
-
question_answer10)
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is: (CBSE 2011)
A)
4 units done
clear
B)
\[\pi \]units done
clear
C)
8 units done
clear
D)
2 units done
clear
View Solution play_arrow
-
question_answer11)
If the difference between the circumference and the radius of a circle is \[\text{37 cm},\] then using \[\pi =\frac{22}{7}\] the circumference (in cm) of the circle is: (CBSE 2013)
A)
154 done
clear
B)
44 done
clear
C)
14 done
clear
D)
7 done
clear
View Solution play_arrow
-
question_answer12)
If \[\pi \] is taken as \[\frac{22}{7},\] the distance (in metres) covered by a wheel of diameter \[\text{35 cm},\] in one revolution, is: (C8SE 2013)
A)
\[2.2\] done
clear
B)
\[1.1\] done
clear
C)
\[\text{9}.\text{625}\] done
clear
D)
\[\text{96}.\text{25}\] done
clear
View Solution play_arrow
-
question_answer13)
If the circumferences of two circles are in the ratio \[\text{4}:\text{9},\]then the ratio in their area is: (CBSE 2013)
A)
\[9:4\] done
clear
B)
\[4:9\] done
clear
C)
\[2:3\] done
clear
D)
\[\text{16}:\text{81}\] done
clear
View Solution play_arrow
-
question_answer14)
If the circumference of a circle is 352 metres, then its area in square metres is:
A)
5986 done
clear
B)
6589 done
clear
C)
7952 done
clear
D)
9856 done
clear
View Solution play_arrow
-
question_answer15)
The areas of two concentric circles forming a ring are 154 square cm and 616 square cm. The breadth of the ring is:
A)
\[\frac{7}{2}\,cm\] done
clear
B)
\[14\,cm\] done
clear
C)
\[7\,cm\] done
clear
D)
\[21\,cm\] done
clear
View Solution play_arrow
-
question_answer16)
The diameter of a wheel is\[\text{1}.\text{26 m}\]. How far will it travel in 500 revolutions?
A)
\[\text{267}0\,\text{m}\] done
clear
B)
\[\text{288}0\text{ m}\] done
clear
C)
\[\text{198}0\text{ m}\] done
clear
D)
\[\text{1596}\,\text{m}\] done
clear
View Solution play_arrow
-
question_answer17)
If the wheel of an engine of a train is \[4\frac{2}{7}\,m\] in circumference makes seven revolutions in 4 seconds, then the speed of the train is:
A)
\[\text{25km}/\text{h}\] done
clear
B)
C)
\[\text{27 km}/\text{h}\] done
clear
D)
\[\text{30 km}/\text{h}\] done
clear
View Solution play_arrow
-
question_answer18)
Atoothed wheel of diameter is attached to a smaller wheel of diameter\[\text{3}0\text{ cm}\]. How many revolutions will the smaller wheel make when the larger one makes 15 revolutions?
A)
23 done
clear
B)
24 done
clear
C)
25 done
clear
D)
26 done
clear
View Solution play_arrow
-
question_answer19)
The difference between the circumference and the radius of a circle is\[\text{37 cm}\]. The area of the circle is:
A)
\[\text{149 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{154 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{121 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{169 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer20)
The circumferences of two concentric circles forming a ring are \[\text{88 cm}\] and 66 respectively. The width of the ring is:
A)
\[14\,cm\] done
clear
B)
\[7\,cm\] done
clear
C)
\[\frac{7}{2}\,cm\] done
clear
D)
\[21\,cm\] done
clear
View Solution play_arrow
-
question_answer21)
The diameter of the wheel of a bus is\[\text{1}.\text{4 m}\]. The wheel makes 10 revolutions in 5 seconds. The speed of the vehicle (in kmph) is:
A)
30 done
clear
B)
31 done
clear
C)
\[\text{31}.\text{68}\] done
clear
D)
35 done
clear
View Solution play_arrow
-
question_answer22)
The number of rounds that a wheel of diameter \[\frac{7}{11}m\] will make in going \[\text{4 km}\] is:
A)
1500 done
clear
B)
1700 done
clear
C)
2000 done
clear
D)
2500 done
clear
View Solution play_arrow
-
question_answer23)
A circular wire of radius \[\text{42 cm}\] is cut and bent into the form of a rectangle whose sides are in the ratio of\[\text{6}:\text{5}\]. The smaller side of the rectangle is:
A)
\[30\,cm\] done
clear
B)
\[60\,cm\] done
clear
C)
\[70\,cm\] done
clear
D)
\[80\,cm\] done
clear
View Solution play_arrow
-
question_answer24)
Match the columns:
| 1. Area of quadrant | (A) \[\frac{1}{2}\pi {{r}^{2}}\] |
| 2. Area of equilateral triangle | (B) \[\frac{\sqrt{3}}{4}\times sid{{e}^{2}}\] |
| 3. Area of semicircle | (C) \[\frac{\sqrt{3}}{2}sid{{e}^{2}}\] |
| 4. Perimeter of semicircle | (D) \[\frac{1}{4}\,\pi {{r}^{2}}\] |
| | (E) 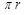 |
| | (F) \[\,\pi r+2r\] |
A)
1\[\to \]A, 2\[\to \]C, 3\[\to \]D, 4\[\to \]E done
clear
B)
1\[\to \]B, 2\[\to \]C, 3\[\to \]F, 4\[\to \]E done
clear
C)
1\[\to \]D, 2\[\to \]B, 3\[\to \]A, 4\[\to \]F done
clear
D)
1\[\to \]D, 2\[\to \]B, 3\[\to \]E, 4\[\to \]F done
clear
View Solution play_arrow
-
question_answer25)
The outer and inner diameters of a circular ring are \[\text{34 cm}\]and \[\text{32 cm,}\] respectively. Then, the area of ring is:
A)
\[\text{1}0\text{3}.\text{71 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{94}\text{.61 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{1}0\text{5}.\text{43 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{97}.\text{93 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer26)
The area of a quadrant of a circle whose circumference is 22 cm, is: \[\left( use\,\,\,\pi =\frac{22}{7} \right)\] (NCERT EXERCISE; CBSE 2013)
A)
\[\frac{77}{8}c{{m}^{2}}\] done
clear
B)
\[\frac{67}{8}c{{m}^{2}}\] done
clear
C)
\[\frac{83}{8}c{{m}^{2}}\] done
clear
D)
\[\frac{55}{8}c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer27)
Two circles touch internally. The sum of their areas is \[116\pi \,c{{m}^{2}}\] and the distance between their centres is\[\text{6 cm}\]. The radii of the circles, are: (CBSE 2017)
A)
\[\text{4 cm},\text{1}0\text{ cm}\] done
clear
B)
\[\text{2 cm},6\text{ cm}\] done
clear
C)
\[\text{3 cm},5\text{ cm}\] done
clear
D)
\[\text{5 cm},8\text{ cm}\] done
clear
View Solution play_arrow
-
question_answer28)
If r is the radius of a circle, then the circumference of the circle is:
A)
\[\pi r\] done
clear
B)
\[2\pi r\] done
clear
C)
\[\pi {{r}^{2}}\] done
clear
D)
\[\frac{1}{2}\pi {{r}^{2}}\] done
clear
View Solution play_arrow
-
question_answer29)
If r is the radius of a circle, then the area of the circle is:
A)
\[\pi r\] done
clear
B)
\[2\pi r\] done
clear
C)
\[\pi {{r}^{2}}\] done
clear
D)
\[\frac{1}{2}\pi {{r}^{2}}\] done
clear
View Solution play_arrow
-
question_answer30)
What is the ratio between the circumference and diameter of a circle of radius r?
A)
\[\pi :1\] done
clear
B)
\[1:\pi \] done
clear
C)
\[1:2\] done
clear
D)
\[2:1\] done
clear
View Solution play_arrow
-
question_answer31)
Length of the arc of a semicircle of radius r is:
A)
\[2\pi r\] done
clear
B)
\[\pi r\] done
clear
C)
\[2r\] done
clear
D)
\[r\] done
clear
View Solution play_arrow
-
question_answer32)
Length of the arc of a quadrant of a circle of radius r is:
A)
\[\frac{\pi r}{2}\] done
clear
B)
\[\pi r\] done
clear
C)
\[2\pi r\] done
clear
D)
\[\frac{\pi r}{2}+2r\] done
clear
View Solution play_arrow
-
question_answer33)
If the perimeter and the area of a circle are equal numerically, then the diameter of the circle is: (NCERT EXERCISE)
A)
\[\text{2 units}\] done
clear
B)
\[\pi \text{ units}\] done
clear
C)
\[\text{4 units}\] done
clear
D)
\[\text{7 units}\] done
clear
View Solution play_arrow
-
question_answer34)
The area of an annulus, whose internal and external radii are \[{{r}_{1}}\] and \[{{r}_{2}}\] respectively, is:
A)
\[\pi (r_{2}^{2}-r_{1}^{2})\] done
clear
B)
\[\pi ({{r}_{2}}+{{r}_{1}})\] done
clear
C)
\[\pi ({{r}_{2}}-{{r}_{1}})\] done
clear
D)
\[\pi \,{{r}_{1}}{{r}_{2}}\] done
clear
View Solution play_arrow
-
question_answer35)
The radius of a circle is\[\text{21 cm}\]. Find its area.
A)
\[1386\,c{{m}^{2}}\] done
clear
B)
\[2\pi \,(21)\] done
clear
C)
\[\frac{\pi }{2}\,{{(21)}^{2}}\] done
clear
D)
\[\frac{\pi }{4}\,{{(21)}^{2}}\] done
clear
View Solution play_arrow
-
question_answer36)
The radius of a circle is\[\text{21 cm}\]. Find its circumference.
A)
\[\text{66 cm}\] done
clear
B)
\[\text{33 cm}\] done
clear
C)
\[\text{132 cm}\] done
clear
D)
\[\text{99 cm}\] done
clear
View Solution play_arrow
-
question_answer37)
Find the radius of the circle whose circumference is\[\text{176 cm}\].
A)
\[\text{7 cm}\] done
clear
B)
\[\text{14 cm}\] done
clear
C)
\[\text{21cm}\] done
clear
D)
\[\text{28 cm}\] done
clear
View Solution play_arrow
-
question_answer38)
Find the radius of the circle whose area is\[\text{154 c}{{\text{m}}^{\text{2}}}\].
A)
\[\text{7 cm}\] done
clear
B)
\[\text{14 cm}\] done
clear
C)
\[\text{21cm}\] done
clear
D)
\[\text{28 cm}\] done
clear
View Solution play_arrow
-
question_answer39)
The radius of a semicircular compound is\[\text{35 m}\]. Find its perimeter.
A)
\[\text{45 m}\] done
clear
B)
\[\text{90 m}\] done
clear
C)
\[\text{135 m}\] done
clear
D)
\[\text{180 m}\] done
clear
View Solution play_arrow
-
question_answer40)
The diameter of a semicircle is 8 cm. Its area is:
A)
\[2\pi c{{m}^{2}}\] done
clear
B)
\[4\pi c{{m}^{2}}\] done
clear
C)
\[8\pi c{{m}^{2}}\] done
clear
D)
\[16\pi c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer41)
The radii of two concentric circles are \[6\,cm\] and \[4\,cm\].Find the ratio of their areas.
A)
\[9:4\] done
clear
B)
\[3:4\] done
clear
C)
\[9:2\] done
clear
D)
\[9:16\] done
clear
View Solution play_arrow
-
question_answer42)
Find the perimeter of a quadrant of a circle of radius\[\text{7 cm}\].
A)
\[\text{10 cm}\] done
clear
B)
\[\text{15 cm}\] done
clear
C)
\[\text{20 cm}\] done
clear
D)
\[\text{25 cm}\] done
clear
View Solution play_arrow
-
question_answer43)
The ratio of the areas of a circle and an equilateral triangle, whose diameter and side are equal, is:
A)
\[\sqrt{3}:\pi \] done
clear
B)
\[\pi :\sqrt{2}\] done
clear
C)
\[\pi :\sqrt{3}\] done
clear
D)
\[\pi :1\] done
clear
View Solution play_arrow
-
question_answer44)
A wire is in the shape of a circle of radius\[\text{42 cm}\]. It is bent into a square. The side of the square is:
A)
\[\text{11 cm}\] done
clear
B)
\[\text{22}\,\text{cm}\] done
clear
C)
\[33\,\text{cm}\] done
clear
D)
\[66\,\text{cm}\] done
clear
View Solution play_arrow
-
question_answer45)
A bicycle wheel makes 5000 revolutions in moving \[\text{11 km}\]. Find the circumference of the wheel.
A)
\[55\,cm\] done
clear
B)
\[110\,cm\] done
clear
C)
\[165\,cm\] done
clear
D)
\[220\,cm\] done
clear
View Solution play_arrow
-
question_answer46)
If a circular grass lawn of \[\text{35 m}\] in radius has a path \[\text{7 m}\]. wide running around it on the outside, then the area of the path is:
A)
\[\text{145}0\,{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{1576 }{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{1694 }{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{3368 }{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer47)
If the area of a semi-circular field is \[\text{154}00\text{ sq m},\] then perimeter of the field is:
A)
\[160\sqrt{2}\,m\] done
clear
B)
\[260\sqrt{2}\,m\] done
clear
C)
\[360\sqrt{2}\,m\] done
clear
D)
\[460\sqrt{2}\,m\] done
clear
View Solution play_arrow
-
question_answer48)
The sum of the areas of two circle, which touch each other externally, is \[153\pi \]. If the sum of their radii is 15, then the ratio of the Larger to the smaller radius is:
A)
\[4:1\] done
clear
B)
\[2:1\] done
clear
C)
\[3:1\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer49)
If the sum of the circumferences of two circles with diameters\[{{d}_{1}}\]and\[{{d}_{2}}\] is equal to the circumference of a circle of diameter d, then
A)
\[d_{1}^{2}+d_{2}^{2}={{d}^{2}}\] done
clear
B)
\[{{d}_{1}}+{{d}_{2}}=d\] done
clear
C)
\[{{d}_{1}}+{{d}_{2}}>d\] done
clear
D)
\[{{d}_{1}}+{{d}_{2}}<d\] done
clear
View Solution play_arrow
-
question_answer50)
If the circumference of a circle increases from \[4\pi \]to \[8\pi \], then its area is:
A)
halved done
clear
B)
doubled done
clear
C)
tripled done
clear
D)
quadrupled done
clear
View Solution play_arrow
-
question_answer51)
If the perimeter of a semi-circular protractor is \[\text{56 cm},\] then its diameter is:
A)
\[\text{10 cm}\] done
clear
B)
\[\text{14 cm}\] done
clear
C)
\[\text{12 cm}\] done
clear
D)
\[\text{16 cm}\] done
clear
View Solution play_arrow
-
question_answer52)
The circumference of a circle is equal to the sum of the circumferences of two circles having diameters \[\text{34 cm}\] and\[\text{1}0\text{ cm}\]. The radius of the new circle is: (NCERT EXEMPLAR)
A)
\[\text{14 cm}\] done
clear
B)
\[\text{28 cm}\] done
clear
C)
\[\text{22 cm}\] done
clear
D)
\[\text{44 cm}\] done
clear
View Solution play_arrow
-
question_answer53)
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of \[\pi ,\] is:
A)
\[\pi :\sqrt{3}\] done
clear
B)
\[2:\sqrt{\pi }\] done
clear
C)
\[3:\pi \] done
clear
D)
\[\pi :\sqrt{2}\] done
clear
View Solution play_arrow
-
question_answer54)
If area of a circular path of uniform width h surrounding a circular region of radius r is:
A)
\[\pi (2r+h)r\] done
clear
B)
\[\pi (2r+h)h\] done
clear
C)
\[\pi (h+r)r\] done
clear
D)
\[\pi (h+r)h\] done
clear
View Solution play_arrow
-
question_answer55)
While making 1000 revolutions, a wheel covers\[\text{88 km}\]. The diameter of the wheel is:
A)
\[\text{14 m}\] done
clear
B)
\[\text{24 m}\] done
clear
C)
\[\text{28 m}\] done
clear
D)
\[\text{40 m}\] done
clear
View Solution play_arrow
-
question_answer56)
A steel wire when bent in the form of a square encloses an area of\[121c{{m}^{2}}\]. If the same wire is bent in the form of a circle, then the circumference of the circle is:
A)
\[88\,cm\] done
clear
B)
\[44\,cm\] done
clear
C)
\[22\,cm\] done
clear
D)
\[11\,cm\] done
clear
View Solution play_arrow
-
question_answer57)
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is \[132\,m\]. The width of path is:
A)
\[20\,m\] done
clear
B)
\[21\,m\] done
clear
C)
\[22\,m\] done
clear
D)
\[24\,m\] done
clear
View Solution play_arrow
-
question_answer58)
The external and internal diameters of a circular path are \[12\,m\] and \[8\,m\] respectively. The area of the circular path is:
A)
\[9\pi \,{{m}^{2}}\] done
clear
B)
\[16\pi \,{{m}^{2}}\] done
clear
C)
\[20\pi \,{{m}^{2}}\] done
clear
D)
\[36\pi \,{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer59)
The sum of radii of two different wheels of a tractor is \[\text{98 cm}\] and the difference of their circumferences is\[\text{176 cm}\]. Find the diameter of the bigger wheel.
A)
\[\text{128 cm}\] done
clear
B)
\[\text{126 cm}\] done
clear
C)
\[\text{63 cm}\] done
clear
D)
\[\text{64 cm}\] done
clear
View Solution play_arrow
-
question_answer60)
The radius of a circle is\[\text{2}0\text{ cm}\]. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is: (Take \[\pi =3.14\])
A)
\[10\sqrt{5}\,cm\] done
clear
B)
\[10\sqrt{3}\,cm\] done
clear
C)
\[10\,cm\] done
clear
D)
\[10\sqrt{2}\,cm\] done
clear
View Solution play_arrow
-
question_answer61)
A race track is in the form of a circular ring whose outer and inner circumferences are \[\text{396 m}\] and \[\text{352}\,\text{m}\] respectively. The width of the track is:
A)
\[63\,\text{m}\] done
clear
B)
\[56\,\text{m}\] done
clear
C)
\[7\,\text{m}\] done
clear
D)
\[3.5\,\text{m}\] done
clear
View Solution play_arrow
-
question_answer62)
There are five circular windows each of radius \[35\,c\text{m}\] are to be fitted with glass. Find the cost of glass at the rate of Rs.155 per sq. m.
A)
\[\text{Rs}.\text{223}.\text{5}0\] done
clear
B)
\[\text{Rs}\text{. 298}.\text{37}\] done
clear
C)
\[\text{Rs}\text{.353}.\text{17}\] done
clear
D)
\[\text{Rs}.\text{192}.\text{53}\] done
clear
View Solution play_arrow
-
question_answer63)
The radii of two concentric circles are \[19\,cm\]and \[16\,cm\]respectively. The area of the ring enclosed by these circles is:
A)
\[\text{32}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{33}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{352 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{350 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer64)
In a circle of radius \[\text{35 cm}\] an arc subtends an angle of \[30{}^\circ \]at the centre. The Length of the arc is:
A)
\[\frac{11}{21}\,cm\] done
clear
B)
\[\frac{55}{3}\,cm\] done
clear
C)
\[\frac{55}{21}\,cm\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer65)
The sum of areas of three sectors of radius r formed at the vertices of a triangle is:
A)
\[2\pi {{r}^{2}}\] done
clear
B)
\[\pi {{r}^{2}}\] done
clear
C)
\[\frac{\pi {{r}^{2}}}{2}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer66)
A cow is tied to a peg at one corner of a rectangular field of dimensions \[10\,m\times 8\,m\] by a \[3\,m\] long rope. The area of the part of the field in which the cow can graze is:
A)
\[14.14\,{{m}^{2}}\] done
clear
B)
\[7.07\,{{m}^{2}}\] done
clear
C)
\[6.07\,{{m}^{2}}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer67)
The region bounded by a chord and the corresponding arc of the circle is called the ......... of the circle.
A)
segment done
clear
B)
sector done
clear
C)
arc done
clear
D)
radius done
clear
View Solution play_arrow
-
question_answer68)
The area of the sector of a circle of radius \[\text{6 cm}\] whose central angle is \[30{}^\circ ,\] is: (Taken\[=\text{3}.\text{14}\]) (CBSE 2020)
A)
\[\text{9}.\text{42 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{1}0.\text{32 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{1}0.\text{58 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{11}.\text{52 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
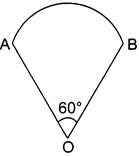
question_answer69)
| In fig., OAB is a sector of circle of radius\[\text{1}0.\text{5}~~\text{cm}\].The perimeter or Circumference of the sector is \[\left( Take\,\,\pi =\frac{22}{7} \right)\] (CBSE 2020) |
 |
A)
\[30\,cm\] done
clear
B)
\[32\,cm\] done
clear
C)
\[34\,cm\] done
clear
D)
\[36\,cm\] done
clear
View Solution play_arrow
-
question_answer70)
Match the columns:
| 1. | Area of sector | (A) | \[\frac{1}{2}\times \pi {{r}^{2}}\] |
| 2. | Perimeter of sector | (B) | \[\frac{\theta }{360{}^\circ }\times \pi {{r}^{2}}\] |
| 3. | Area of major segment | (C) | Area of circle-area of minor segment |
| 4. | Perimeter of minor segment | (D) | \[2r+length\,\,of\,arc\] |
| | | (E) | length of arc + length of corresponding chord. |
A)
1\[\to \]B, 2\[\to \]C, 3\[\to \]D, 4\[\to \]E done
clear
B)
1\[\to \]B, 2\[\to \]D, 3\[\to \]C, 4\[\to \]E done
clear
C)
1\[\to \]A, 2\[\to \]C, 3\[\to \]D, 4\[\to \]E done
clear
D)
1\[\to \]B, 2\[\to \]C, 3\[\to \]D, 4\[\to \]E done
clear
View Solution play_arrow
-
question_answer71)
Area of a sector of a circle of radius \[36\,cm\] is\[\text{5471 cm}{{\text{ }}^{\text{2}}}\]. The length of the corresponding arc of the sector is: (NCERT EXEMPIAR, CBSE2011,17)
A)
\[6.44\,cm\] done
clear
B)
\[\text{7}.\text{53 cm}\] done
clear
C)
\[\text{8}.\text{69 cm}\] done
clear
D)
\[\text{9}.\text{43 cm}\] done
clear
View Solution play_arrow
-
question_answer72)
The Length of the minute hand of a clock is\[\text{7 cm}\]. The area swept by the minute hand in 5 minutes, is: (CBSE 2013)
A)
\[\text{12}.\text{83 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{1}0.\text{33 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{9}\text{.53 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{11}.\text{37 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer73)
Length of an arc of a sector of a circle of radius r and angle with degree measure \[\theta \] is:
A)
\[\frac{\theta }{360{}^\circ }\times 2\pi r\] done
clear
B)
\[\frac{\theta }{360{}^\circ }\times \pi {{r}^{2}}\] done
clear
C)
\[\frac{\theta }{360{}^\circ }\times \frac{\pi {{r}^{2}}}{2}\] done
clear
D)
\[\frac{\theta }{360{}^\circ }\times \frac{\pi {{r}^{2}}}{4}\] done
clear
View Solution play_arrow
-
question_answer74)
Find the angle through which the minute hand of a clock moves from \[\text{6 p}.\text{m}.\] to\[\text{6}.\text{55 pm}\].
A)
\[60{}^\circ \] done
clear
B)
\[45{}^\circ \] done
clear
C)
\[90{}^\circ \] done
clear
D)
\[210{}^\circ \] done
clear
View Solution play_arrow
-
question_answer75)
The radius of a circle is\[\text{5 cm}\]. Find the area of the sector formed by an arc of this circle of length \[\text{9 cm}\].
A)
\[45\,c{{m}^{2}}\] done
clear
B)
\[22.5\,c{{m}^{2}}\] done
clear
C)
\[67.5\,c{{m}^{2}}\] done
clear
D)
\[2.25\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer76)
The measure of the central angle of a circle is
A)
\[45{}^\circ \] done
clear
B)
\[90{}^\circ \] done
clear
C)
\[180{}^\circ \] done
clear
D)
\[360{}^\circ \] done
clear
View Solution play_arrow
-
question_answer77)
The central angle of a quadrant of a circle measures:
A)
\[90{}^\circ \] done
clear
B)
\[135{}^\circ \] done
clear
C)
\[45{}^\circ \] done
clear
D)
\[180{}^\circ \] done
clear
View Solution play_arrow
-
question_answer78)
What is the supplementary angle of the central angle of a semicircle?
A)
\[0{}^\circ \] done
clear
B)
\[90{}^\circ \] done
clear
C)
\[180{}^\circ \] done
clear
D)
\[360{}^\circ \] done
clear
View Solution play_arrow
-
question_answer79)
Find the area of the major segment of a circle of the area of the minor segment is \[\text{25}\,\text{c}{{\text{m}}^{2}}\] and the area of the circle is \[100\,\text{c}{{\text{m}}^{2}}\].
A)
\[25\,\text{c}{{\text{m}}^{2}}\] done
clear
B)
\[100\,\text{c}{{\text{m}}^{2}}\] done
clear
C)
\[75\,\text{c}{{\text{m}}^{2}}\] done
clear
D)
\[50\,\text{c}{{\text{m}}^{2}}\] done
clear
View Solution play_arrow
-
question_answer80)
The minute hand of a clock is of length \[\text{4 cm}\] Find the angle swept by the minute hand in 15 minutes.
A)
\[90{}^\circ \] done
clear
B)
\[30{}^\circ \] done
clear
C)
\[45{}^\circ \] done
clear
D)
\[60{}^\circ \] done
clear
View Solution play_arrow
-
question_answer81)
A sector is cut from a circular sheet of radius \[100\,cm,\] the angle of the sector being \[240{}^\circ \]. if another circle of the area same as the sector is formed, then radius of the new circle is:
A)
\[\text{79}.\text{5 cm}\] done
clear
B)
\[\text{81}.\text{5 cm}\] done
clear
C)
\[\text{83}.\text{4 cm}\] done
clear
D)
\[\text{88}.\text{5 cm}\] done
clear
View Solution play_arrow
-
question_answer82)
The ratio of the outer and inner circumference of a circular path is\[\text{23}:\text{22}\]. If the path is 5 meters wide, the diameter of the inner circle is:
A)
\[55\,m\] done
clear
B)
\[110\,m\] done
clear
C)
\[220\,m\] done
clear
D)
\[230\,m\] done
clear
View Solution play_arrow
-
question_answer83)
Priyanshu has a motor cycle with wheels of diameter\[\text{91 cm}\]. There are 22 spokes in the wheel. Find the length of arc between two adjoining spokes.
A)
\[\text{26 cm}\] done
clear
B)
\[\text{13 cm}\] done
clear
C)
\[\text{15 cm}\] done
clear
D)
\[\text{18 cm}\] done
clear
View Solution play_arrow
-
question_answer84)
A pendulum swings through an angle of \[60{}^\circ \] and describes an arc \[\text{8}.\text{8 cm}\] in Length. The length of pendulum is:
A)
\[4.2\,cm\] done
clear
B)
\[2.1\,cm\] done
clear
C)
\[8.4\,cm\] done
clear
D)
\[6.3\,cm\] done
clear
View Solution play_arrow
-
question_answer85)
The area of the sector of a circle of radius R making a central angle of x is: (NCERT EXEMPLAR; NCERT EXERCISE)
A)
\[\frac{x}{180{}^\circ }\times 2\pi R\] done
clear
B)
\[\frac{x}{360{}^\circ }\times 2\pi R\] done
clear
C)
\[\frac{x}{180{}^\circ }\times \pi {{R}^{2}}\] done
clear
D)
\[\frac{x}{360{}^\circ }\times \pi {{R}^{2}}\] done
clear
View Solution play_arrow
-
question_answer86)
A sector of a circle of diameter \[\text{8 cm}\] contains an angle of \[135{}^\circ \]. The area of sector is:
A)
\[6\pi \,c{{m}^{2}}\] done
clear
B)
\[6\,c{{m}^{2}}\] done
clear
C)
\[12\pi \,c{{m}^{2}}\] done
clear
D)
\[20\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer87)
The sum of areas of a major sector and the corresponding minor sector of a circle is equal to:
A)
area of the circle done
clear
B)
\[1/2\] (area of the circle) done
clear
C)
\[1/4\] (area of the circle) done
clear
D)
\[3/4\] (area of the circle) done
clear
View Solution play_arrow
-
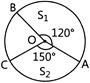
question_answer88)
| In the given figure, the ratio of the areas of two sectors \[{{S}_{1}}\] and \[{{S}_{2}}\] is: |
 |
A)
\[5:2\] done
clear
B)
\[3:5\] done
clear
C)
\[5:3\] done
clear
D)
\[4:5\] done
clear
View Solution play_arrow
-
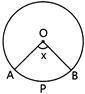
question_answer89)
| In the following figure, O is the centre of the circle. The area of the sector OAPB is \[\frac{5}{12}\] part of the area of the circle. Find the value of x. |
 |
A)
\[130{}^\circ \] done
clear
B)
\[60{}^\circ \] done
clear
C)
\[45{}^\circ \] done
clear
D)
\[150{}^\circ \] done
clear
View Solution play_arrow
-
question_answer90)
The length of the minute hand of a clock is \[\sqrt{21}\,cm.\]Find the area swept by the minute hand from \[\text{9 a}.\text{m}.\] to \[\text{9}.\text{1}0\text{ a}.\text{m}.\]
A)
\[\text{22 c}{{\text{m}}^{2}}\] done
clear
B)
\[\text{11 c}{{\text{m}}^{2}}\] done
clear
C)
\[\text{45 c}{{\text{m}}^{2}}\] done
clear
D)
\[\text{31 c}{{\text{m}}^{2}}\] done
clear
View Solution play_arrow
-
question_answer91)
A car has two wipers which do not overlap. Each wiper has a blade of Length \[\text{42 cm}\] sweeping through an angle of \[120{}^\circ \]. Find the total area cleaned at each sweep of the blades.
A)
\[\text{4224 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{3696 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{1848 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{5544 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer92)
A chord of a circle of radius \[\text{28 cm}\] subtends an angle of \[60{}^\circ \]at the centre of the circle. The area of the minor segment is: (Take \[\sqrt{3}=1.732\])
A)
\[60.256\,c{{m}^{2}}\] done
clear
B)
\[339.47\,c{{m}^{2}}\] done
clear
C)
\[410.67\,c{{m}^{2}}\] done
clear
D)
\[71.20\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer93)
A chord of a circle subtends an angle of \[60{}^\circ \] at the centre of the circle. If the length of the chord is \[\text{1}0\text{ cm},\] then the area of the major segment is: (Take \[\pi =3.14\] and \[\sqrt{3}=1.732\])
A)
\[304.97\,c{{m}^{2}}\] done
clear
B)
\[295\,c{{m}^{2}}\] done
clear
C)
\[310\,c{{m}^{2}}\] done
clear
D)
\[335\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer94)
The area of the square that can be inscribed in a circle of radius 8 cm is: (NCERT EXEMPLAR)
A)
\[256\,c{{m}^{2}}\] done
clear
B)
\[128\,c{{m}^{2}}\] done
clear
C)
\[64\sqrt{2}\,c{{m}^{2}}\] done
clear
D)
\[64\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer95)
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is: (CBSE 2011)
A)
\[4a\] done
clear
B)
\[5a\] done
clear
C)
\[8a\] done
clear
D)
\[10a\] done
clear
View Solution play_arrow
-
question_answer96)
| Find the area of the shaded region in fig. If \[\text{PQ}=\text{24 cm},\] \[\text{PR}=\text{7 cm}\] and O is the centre of the circle. (NCERT EXERCISE; CBSE 2020) |
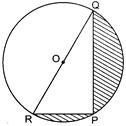 |
A)
\[161.54\,c{{m}^{2}}\] done
clear
B)
\[165.63\,c{{m}^{2}}\] done
clear
C)
\[167.24\,c{{m}^{2}}\] done
clear
D)
\[169.43\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer97)
| In the given figure, three sectors of a circle of radius x\[7cm\] .making angles of \[60{}^\circ ,\] \[80{}^\circ \] and \[40{}^\circ \] at the centre are shaded. The area of the shaded region (in \[c{{m}^{2}}\]) is \[\left[ \text{Using }\pi \text{=}\frac{22}{7} \right]\](C6SE 2012) |
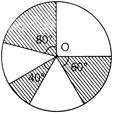 |
A)
77 done
clear
B)
154 done
clear
C)
44 done
clear
D)
22 done
clear
View Solution play_arrow
-
question_answer98)
The area of the largest circle that can be drawn inside a square of side \[\text{14 cm}\] in length is:
A)
\[\text{121 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{154 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{169 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{196 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer99)
The area of the Largest circle that can be drawn inside a rectangle with sides \[\text{7 m }\times \text{3}.\text{5 m}\] is:
A)
\[\frac{77}{2}{{m}^{2}}\] done
clear
B)
\[77\,{{m}^{2}}\] done
clear
C)
\[\frac{77}{8}\,{{m}^{2}}\] done
clear
D)
\[\frac{77}{4}\,{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer100)
The area of the largest possible square inscribed in a circle of unit radius (in sq. units) is:
A)
\[\pi \] done
clear
B)
\[\frac{\pi }{2}\] done
clear
C)
\[2\sqrt{2}\] done
clear
D)
\[2\] done
clear
View Solution play_arrow
-
question_answer101)
The ratio of the areas of the incircle and circumcircle of a square is:
A)
\[1:2\] done
clear
B)
\[1:3\] done
clear
C)
\[1:4\] done
clear
D)
\[1:\sqrt{2}\] done
clear
View Solution play_arrow
-
question_answer102)
The ratio of areas of incircle and circumcircle of an equilateral triangle is:
A)
\[1:2\] done
clear
B)
\[1:3\] done
clear
C)
\[1:4\] done
clear
D)
\[1:9\] done
clear
View Solution play_arrow
-
question_answer103)
O is the centre of a circle of radius\[\text{5 cm}\]. The chord AB subtends an angle \[60{}^\circ \] at the centre. Area of the shaded portion is equal to (approximately):
A)
\[50c{{m}^{2}}\] done
clear
B)
\[62.78\,c{{m}^{2}}\] done
clear
C)
\[49.88\,c{{m}^{2}}\] done
clear
D)
\[67.67\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer104)
| ABC is an equilateral triangle. The area of the shaded region if the radius of each of the circle is \[\text{1 cm},\] is: |
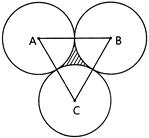 |
A)
\[2-\frac{\pi }{3}\] done
clear
B)
\[\sqrt{3}-\pi \] done
clear
C)
\[\sqrt{3}-\frac{\pi }{2}\] done
clear
D)
\[\sqrt{3}-\frac{\pi }{4}\] done
clear
View Solution play_arrow
-
question_answer105)
| ABCDEF is any hexagon with different vertices A, B, C, D, E and F as the centres of circles with same radius r are drawn. The area of the shaded portion is: |
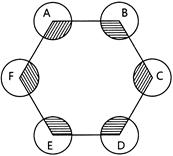 |
A)
\[\pi {{r}^{2}}\] done
clear
B)
\[2\pi {{r}^{2}}\] done
clear
C)
\[3\pi {{r}^{2}}\] done
clear
D)
\[4\pi {{r}^{2}}\] done
clear
View Solution play_arrow
-
question_answer106)
The area of the largest triangle that can be inscribed in a semicircle of radius 21 is: (CBSE 2017)
A)
\[221\,c{{m}^{2}}\] done
clear
B)
\[331\,c{{m}^{2}}\] done
clear
C)
\[441\,c{{m}^{2}}\] done
clear
D)
\[555\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer107)
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
A)
\[2:\pi \] done
clear
B)
\[\pi :2\] done
clear
C)
\[\pi :4\] done
clear
D)
\[4:\pi \] done
clear
View Solution play_arrow
-
question_answer108)
| In figure, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side \[\text{12 cm},\] (Use \[\pi =3.14\]) the area of the shaded region is: (NCERT EXEMPLAR; CBSE 2018) |
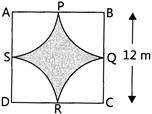 |
A)
\[122\,c{{m}^{2}}\] done
clear
B)
\[144\,c{{m}^{2}}\] done
clear
C)
\[134\,c{{m}^{2}}\] done
clear
D)
\[154\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer109)
| In figure, two concentric circles with centre O, have radii \[21\,cm\] and \[42\,cm\]. If \[\angle \text{AOB}\ \text{=}\ \text{6}{{\text{0}}^{\operatorname{o}}}\] the area of the shaded region is: (CBSE 2017,19) |
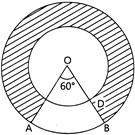 |
A)
\[3465\,c{{m}^{2}}\] done
clear
B)
\[1295\,c{{m}^{2}}\] done
clear
C)
\[2565\,c{{m}^{2}}\] done
clear
D)
\[3980\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer110)
| In the following figure, O is the centre of the circle with \[AC=24\,cm,\] \[\text{AB}=\text{7 cm}\] and \[\angle BOD=90{}^\circ \]. The area of the shaded region, (Use \[\pi =3.14\]) is: (CBSE 2012,17) |
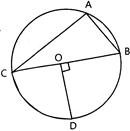 |
A)
\[248\,c{{m}^{2}}\] done
clear
B)
\[284\,c{{m}^{2}}\] done
clear
C)
\[\text{298 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{318 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer111)
| In the given figure, ABCD is a rectangle of dimensions\[\text{21 cm}\times \text{14 cm}\]. A semicircle is drawn with BC as diameter. |
| The area and the perimeter of the shaded region in the figure, are: (CBSE 2017) |
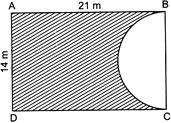 |
A)
\[217\,c{{m}^{2}},\,\,78\,cm\] done
clear
B)
\[215\,c{{m}^{2}},\,\,82\,cm\] done
clear
C)
\[219\,c{{m}^{2}},\,76\,cm\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer112)
The circumference of a circle inscribed in a square of side 14 cm is:
A)
\[11\,cm\] done
clear
B)
\[22\,cm\] done
clear
C)
\[33\,cm\] done
clear
D)
\[44\,cm\] done
clear
View Solution play_arrow
-
question_answer113)
A square circumscribes a circle of radius \[6\,cm\] Find the Length of the diagonal of the square.
A)
\[5\sqrt{2}\,cm\] done
clear
B)
\[12\sqrt{2}\,cm\] done
clear
C)
\[3\sqrt{2}\,cm\] done
clear
D)
\[2\sqrt{2}\,cm\] done
clear
View Solution play_arrow
-
question_answer114)
Find the area of a right angled triangle if the radius of the semicircle is \[\text{5 cm}\] and the altitude drawn to the hypotenuse is \[\text{4 cm}\].
A)
\[8\,c{{m}^{2}}\] done
clear
B)
\[12\,c{{m}^{2}}\] done
clear
C)
\[10\,c{{m}^{2}}\] done
clear
D)
\[20\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer115)
Find the area of a right angled triangle if the diameter of its circumcircle is \[\text{8 cm}\] and altitude drawn to the hypotenuse is\[\text{2}.\text{5 cm}\].
A)
\[10\,c{{m}^{2}}\] done
clear
B)
\[15\,c{{m}^{2}}\] done
clear
C)
\[20\,c{{m}^{2}}\] done
clear
D)
\[30\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer116)
| In the adjoining figure, OABC is a square of side\[\text{7 cm}\]. OAC is a quadrant of a circle with O as centre. The area of the shaded region is: |
 |
A)
\[10.5\,c{{m}^{2}}\] done
clear
B)
\[38.5\,c{{m}^{2}}\] done
clear
C)
\[49\,c{{m}^{2}}\] done
clear
D)
\[11.5\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer117)
| In the given figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O, then the area of the shaded region is: |
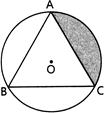 |
A)
\[\frac{5}{3}(5\pi -3\sqrt{3})c{{m}^{2}}\] done
clear
B)
\[\frac{4}{3}(4\pi -3\sqrt{3})c{{m}^{2}}\] done
clear
C)
\[\frac{2}{3}(2\pi -\sqrt{3})c{{m}^{2}}\] done
clear
D)
\[\frac{7}{3}(7\pi -3\sqrt{3})c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer118)
| A square is circumscribing a circle. The side of the square is\[\text{14 cm}\]. Find the area of the shaded region. |
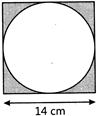 |
A)
\[21c{{m}^{2}}\] done
clear
B)
\[42c{{m}^{2}}\] done
clear
C)
\[48c{{m}^{2}}\] done
clear
D)
\[196c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer119)
All the vertices of a rhombus Lie on a circle. Find the area of the rhombus, if area of the circle is\[706.5c{{m}^{2}}\].(Take \[\pi =3.14\])
A)
\[225\,c{{m}^{2}}\] done
clear
B)
\[450\,c{{m}^{2}}\] done
clear
C)
\[353\,c{{m}^{2}}\] done
clear
D)
\[400\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer120)
| In the figure, ABDCA represents a quadrant of a circle of radius \[\text{7 cm}\]with centre A. Find the area of the shaded portion. |
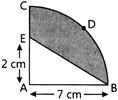 s s |
A)
\[14\,c{{m}^{2}}\] done
clear
B)
\[24.5\,c{{m}^{2}}\] done
clear
C)
\[38.5\,c{{m}^{2}}\] done
clear
D)
\[31.5\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer121)
| A park is in the form of a rectangle of dimensions\[120\,m\times 100\,m\]. In the centre of the park, there is a circular lawn as shown in the figure. The area of the park excluding the lawn is \[8700\,{{m}^{2}}\]. Find the radius of the circular lawn. |
 |
A)
\[32.4\,m\] done
clear
B)
\[36\,m\] done
clear
C)
\[29.6\,m\] done
clear
D)
\[39.4\,m\] done
clear
View Solution play_arrow
-
question_answer122)
| In the given figure, ABCD is a trapezium with \[AB||CD\]. The area of the shaded region is: |
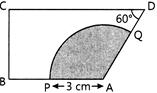 |
A)
\[3\pi \,c{{m}^{2}}\] done
clear
B)
\[6\pi \,c{{m}^{2}}\] done
clear
C)
\[9\pi \,c{{m}^{2}}\] done
clear
D)
\[7\pi \,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer123)
| A playground is in the form of a rectangle having semicircles on the shorter sides, its area, when the length of the rectangular portion is \[\text{7}0\text{ m}\] and the breadth is \[\text{56 m},\] is: |
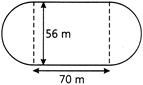 |
A)
\[6274\,{{m}^{2}}\] done
clear
B)
\[7476\,{{m}^{2}}\] done
clear
C)
\[6384\,{{m}^{2}}\] done
clear
D)
\[7274\,{{m}^{2}}\] done
clear
View Solution play_arrow
-
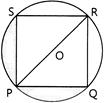
question_answer124)
| In the figure, PQRS is a square, O is centre of the circle. If \[RS=10\sqrt{2}\,cm,\] then area of shaded region is: |
 |
A)
\[(90\pi -90)c{{m}^{2}}\] done
clear
B)
\[(80\pi -80)c{{m}^{2}}\] done
clear
C)
\[(50\pi -100)c{{m}^{2}}\] done
clear
D)
\[(100\pi -100)c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer125)
| PQRS is the diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal. Semi circles are drawn with PQ and QS as diameter as shown in the figure. The ratio of the area of the shaded region to that of the unshaded region is: |
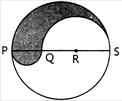 |
A)
\[1:2\] done
clear
B)
\[13:5\] done
clear
C)
\[5:13\] done
clear
D)
\[18:5\] done
clear
View Solution play_arrow
