Speed and Velocity
Category : Railways
Speed and Velocity
REST AND MOTION
Rest: When position of a body does not change with time it is said to be in state of rest.
Motion: When position of a body changes with time it is said to be in state of motion. Rest and motion are relative terms.
(i) Absolute motion: The motion of a body with respect to a body which is at complete rest is called absolute motion which is impossible.
(ii) Relative motion: The motion of a body with respect to a body which is at rest relative to the body is called relative motion.
MOTION IN ONE, TWO AND THREE
DIMENSIONS
Motion in One Dimension
An object moving along a straight line or path is said to have dimensional motion, also known as rectilinear motion.
Examples Motion of a bus on a straight road and motion of a train on a straight track, an object dropped from a certain height above the ground, etc.
Motion in Two Dimensions
An object moving in a plane is said to have two dimensional motion,
Examples: Motion of an insect on a floor, earth revolving around the sun, a billiard ball moving over the billiard table, etc.
Motion in Three Dimensions
An object moving in space is said to have three dimensional motion
Examples: Motion of a Kite. motion of a flying aeroplane or bird, etc.
POSITION, PATH LENGTH AND
DISPLACEMENT
Position
The position of any particle can be given as follows:
In cartesian co-ordianate form: The position of any particle is resented by co-ordinates (x, y, z) or position vector\[(\overrightarrow{r})\]. If a particle is located at point A in frame of reference x, y, z then the position of particle will be
\[\overrightarrow{r}=x\,\hat{i}+y\,\hat{j}\,+z\,\,\hat{k}\]
In polar form: \[x=r\cos \theta ;\,\,y=r\sin \theta \]
\[\overrightarrow{r}=r\cos \theta \,\hat{i}\,+r\sin \theta \,\hat{j}\]
Path Length or Distance
The length of the actual path between initial and final positions of a particle in a given interval of time is called distance covered by the particle. Distance is the actual length of the path. It is the characteristic property of any path i.e. path is always associated when we consider distance between two positions.
Characteristics of distance
(i) It is a scalar quantity
(ii) It depends on the path
(iii) It never reduces with time.
(iv) Distance covered by a particle is always positive and can never be negative or zero.
(v) Dimension: \[\left[ M{}^\circ LT0 \right]\]
(vi) Unit: In C. G S. centimetre (cm), in S.I. system, metre (m).
Displacement
The shortest distance from the initial position to the final position of the particle is called displacement
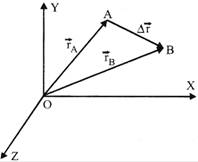
Position vector of Aw.r.t. O=\[\overrightarrow{OA}\]
\[\Rightarrow \] \[\overrightarrow{{{r}_{A}}}={{x}_{1}}\,\,\hat{i}+{{y}_{1}}\,\,\hat{j}+{{z}_{1}}\,\,\hat{k}\]
Position vector of B w.r.t. O\[=\overrightarrow{OB}\]
\[\Rightarrow \] \[\overrightarrow{{{r}_{B}}}={{x}_{2}}\,\,\hat{i}+{{y}_{2}}\,\,\hat{j}+{{z}_{1}}\,\,\hat{k}\]
Displacement \[=\overrightarrow{AB}=({{x}_{2}}-{{x}_{1}})\,\,\hat{i}+({{y}_{2}}-{{y}_{1}})\,\,\hat{j}+({{z}_{2}}-{{z}_{1}})\,\,\hat{k}\]
\[\Delta \overrightarrow{r}=\Delta x\,\,\hat{i}+\Delta y\,\,\hat{j}+\Delta z\,\,\hat{k}\]
Characteristics of displacement
(i) It is a vector quantity.
(ii) The displacement of a particle between any two points is equal to the shortest distance between them.
(iii) The displacement of an object in a given time interval may be \[+ve,\,\,-ve\]or zero.
(iv) The actual distance travelled by a particle in the given interval of time is always equal to or greater than the magnitude of the displacement and in no case, it is less than the magnitude of the displacement, i.e. Distance S Displacement |
(v) Dimension:\[[{{M}^{0}}L{{T}^{0}}]\]
(vi) Unit: In C. G S. centimetre (cm), in S.I. system, metre (m).
SPEED
Speed of an object is defined as the rate of change of position of the object in any direction. It is measured by the distance travelled by the object in unit time in any direction.
(i) It is a scalar quantity
(ii) It gives no idea about the direction of motion of the object.
(iii) It can be zero or positive but never be negative.
(iv) Unit: C.G.S. cm/sec, S.I. m/sec,
(v) Dimensions: \[({{M}^{0}}L{{T}^{-1}})\]
Uniform Speed
An object is said to be moving with a uniform speed, if it covers equal distances in equal intervals of time, howsoever small these intervals may be. The uniform speed is shown by straight line in distance-time graph.
For example, suppose a train travels 1000 m in 60 sec. The train is said to be moving with uniform speed, if it travels 500 m. in 30 sec., 250 m. in 15 sec., 125 m. in 7.5 sec. and soon.
Non-uniform Speed
An object is said to be moving with a non-uniform or variable speed, if it covers equal distances in unequal intervals of time or unequal distances in equal intervals of time, howsoever small these intervals may be.
For example, suppose a train travels first 1000 m in 60 sec, next 1000 m. in 120 sec. and next 1000m. in 50 sec., then the train is moving with variable speed or non-uniform speed.
Average Speed
\[Average\,\,Speed\,\,\overline{V}=\frac{Total\,\,\text{distance}\,\,\text{travelled}}{Total\,\,time\,\,taken}\]
Note:
If any car covers distance \[{{x}_{1,}}\,\,{{x}_{2}},.....{{x}_{n}}\]in the time intervals
\[{{t}_{1}},\,\,{{t}_{2}},.....{{t}_{n}}\] then, average speed,
\[\overline{V}=\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+.....+{{x}_{n}}}{{{t}_{1}}+{{t}_{2}}+.....+{{t}_{n}}}\]
Some important cases related to average speed:
Case 1:
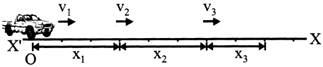
If a car covers distances \[{{x}_{1}},\,\,{{x}_{2}}\,\,and\,\,{{x}_{3}}\]and with speeds \[{{v}_{1}},{{v}_{2}}\,\,and\,\,{{v}_{3}}\] respectively in same direction then average speed of car.
\[\Rightarrow \overline{V}=\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{{{t}_{1}}+{{t}_{2}}+{{t}_{3}}}\,\,;\,\,here,\,\,{{t}_{1}}=\frac{{{x}_{1}}}{{{v}_{1}}},\,\,{{t}_{2}}=\frac{{{x}_{2}}}{{{v}_{2}}},\,\,{{t}_{3}}=\frac{{{x}_{3}}}{{{v}_{3}}}\]
\[\overline{V}=\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{\frac{{{x}_{1}}}{{{v}_{1}}}+\frac{{{x}_{2}}}{{{v}_{2}}}+\frac{{{x}_{3}}}{{{v}_{3}}}}\]
If car covers equal distances with different speeds then,
\[{{x}_{1}}={{x}_{2}}={{x}_{3}}=x\]
\[\overline{V}=\frac{3x}{\frac{x}{{{v}_{1}}}+\frac{x}{{{v}_{2}}}+\frac{x}{{{v}_{3}}}}=\frac{3}{\frac{1}{{{v}_{1}}}+\frac{1}{{{v}_{2}}}+\frac{1}{{{v}_{3}}}}=\frac{3{{v}_{1}}{{v}_{2}}{{v}_{3}}}{{{v}_{1}}{{v}_{2}}+{{v}_{2}}{{v}_{3}}+{{v}_{3}}{{v}_{1}}}\]
Case 2: If anybody travels with speeds during time intervals \[{{t}_{1}},\,\,{{t}_{2}}\] and\[{{t}_{3}}\] respectively then the average speed of the body will be
Average speed \[\overline{V}=\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{{{t}_{1}}+{{t}_{2}}+{{t}_{3}}}=\frac{{{v}_{1}}{{t}_{1}}+{{v}_{2}}{{t}_{2}}+{{v}_{3}}{{t}_{3}}}{{{t}_{1}}+{{t}_{2}}+{{t}_{3}}}\]
\[If\,\,{{t}_{1}}={{t}_{2}}={{t}_{3}}=t\,\,then\,\,\overline{V=\frac{({{v}_{1}}+{{v}_{2}}+{{v}_{3}})\times t}{3\times 1}}\]
\[=\frac{({{v}_{1}}+{{v}_{2}}+{{v}_{3}})}{3}\]
Instantaneous Speed
The speed of the body at any instant of time or at a particular position is called instantaneous speed. Let a body travels a distance \[\Delta x\] in the time interval\[\Delta t\], then its average speed \[=\frac{\Delta x}{\Delta t}\] When\[\Delta t\to 0\], then average speed of the body becomes the instantaneous speed.
\[\therefore \] Instantaneous speed \[=\underset{\Delta t\to 0}{\mathop{Lim}}\,\frac{\Delta x}{\Delta t}=\frac{dx}{dt}\]
Note:
VELOCITY
The rate of change of displacement of a particle with time is called the velocity of the particle.
Displacement
i.e., Velocity\[=\frac{displacement}{Time\,\,\text{interval}}\]
(i) It is a vector quantity
(ii) The velocity of an object can be positive, zero and negative
(iii) Unit: C.G.S. cm/s, S.I. m/s.
(iv) Dimensions: \[[{{M}^{0}}L{{T}^{-1}}]\]
Uniform Velocity
A body is said to move with uniform velocity, if it covers equal displacements in equal intervals of time, howsoever, small these intervals may be.
When a body is moving with uniform velocity, then the magnitude and direction of the velocity of the body remains same at all points of its path.
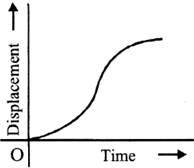
Non-uniform Velocity
The particle is said to move with non-uniform or variable velocity; if it covers unequal displacements in equal intervals of time. Howsoever, small these time intervals may be. In this type of motion velocity does not remain constant. The displacement time graph if a body moving with non-uniform speed is as shown in figure below
Average Velocity
The average velocity of an object is equal to the ratio of the displacement to the time interval for which the motion takes place
i.e.. Average velocity \[=\frac{diplacement}{Time\,\,taken}\]
Instantaneous Velocity
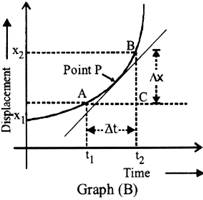
Instantaneous velocity, \[\overrightarrow{V}=\underset{\Delta t\to 0}{\mathop{Lt}}\,\frac{\overrightarrow{\Delta \,\,x}}{\Delta t}=\frac{\overrightarrow{d\,\,x}}{d\,\,t}\]
or inst. velocity at point P
—»
\[\overrightarrow{V}=\tan \alpha \](slope of tangent at point P, graph B)
ACCELERATION
The rate of change of velocity of an object is called acceleration of the object.
Let v and v' be the velocity of the object at time t and t' respectively, then acceleration of the body is given by
Acceleration \[\overrightarrow{(a)}=\frac{Change\,\,in\,\,velocity}{Time\,\,\text{interval}}=\frac{\overrightarrow{v'}-\overrightarrow{v}}{t'-t}\]
Time interval
® It is a vector quantity.
(u) It is positive if the velocity is increasing and is negative if the velocity is decreasing.
(iii) The negative acceleration is also called retardation or deceleration.
(iv) Unit: In S.I. system \[m/{{s}^{2}}\]
In C.G.S. system\[cm/{{m}^{2}}\]
(v) Dimensions: \[[{{M}^{0}}L{{T}^{-2}}]\]
Uniform Acceleration
An object is said to be moving with a uniform acceleration if its velocity changes by equal amounts in equal intervals of time.
Variable Acceleration
An object is said to be moving with a variable acceleration if its velocity changes by unequal amounts in equal intervals of time.
Average Acceleration
When an object is moving with a variable acceleration, then the average acceleration of the object for the given motion is defined as the ratio of the total change in velocity of the object during motion to the total time taken.
Total change in velocity
i.e., Average acceleration \[=\frac{total\,\,change\,\,in\,velocity}{Total\,\,time\,taken}\]
Note:
If anybody is accelerated with acceleration\[\overrightarrow{{{a}_{1}}}\]till time\[{{t}_{1}}\], and acceleration \[\overrightarrow{{{a}_{2}}}\] up to time \[{{t}_{2}}\] then average acceleration, \[\overrightarrow{{{a}_{av}}}=\frac{{{a}_{1}}{{t}_{1}}+{{a}_{2}}{{t}_{2}}}{{{t}_{1}}+{{t}_{2}}}\]
Instantaneous Acceleration
The acceleration of the object at a given instant of time or at a given point of motion, is called its instantaneous acceleration.
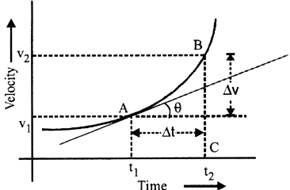
If \[\Delta t\] approaches to zero then the rate of change of velocity will be instantaneous acceleration. Instantaneous acceleration
\[\overrightarrow{{{a}_{inst}}}=\underset{\Delta t\to 0}{\mathop{Lim}}\,\frac{\overrightarrow{\Delta v}}{\Delta t}=\frac{\overrightarrow{d\,\,v}}{d\,\,t}\]
Instantaneous acceleration at a point is equal to slope of tangent at that point on displacement time graph. In the graph shown above this point is given as
\[\overrightarrow{v}=\frac{d\,\,\overrightarrow{x}}{dt}\,\,or,\,\,\overrightarrow{a}=\frac{d}{dt}\,\,\left( \frac{d\,\,\overrightarrow{x}}{dt} \right)=\frac{{{d}^{2}}\overrightarrow{x}}{d{{t}^{2}}}\]
Thus, instantaneous acceleration of an object is equal to the second time derivative of the position of the object at the given instant.
Note:
(i) It is not essential that when velocity is zero acceleration must be zero. Ex. m vertical motion at the top point v = 0 but \[a\ne 0.i.e.,\,\,a=g\] (acceleration due to gravity)
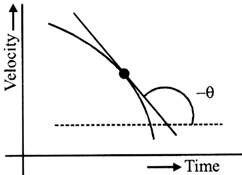
(a) Velocity may vary but \[\frac{dv}{dt}\]may be constant
(ja) The acceleration may vary but v may be constant, e.g. in uniform circular motion.
(iv) If velocity decreases w.r.t. time then acceleration is called retardation.
Retardation \[a=\tan (\pi -\theta )\]
KINEMATIC EQUATIONS FOR UNIFORMLY
ACCELERATED MOTION
\[[v=u+at]\]
In vector form, \[\overrightarrow{v}=\overrightarrow{u}+\overrightarrow{a}t\]
\[[s=ut+\frac{1}{2}a{{t}^{2}}]\]
In vector form, \[\overrightarrow{s}=\overrightarrow{u}t+\frac{1}{2}\overrightarrow{a}{{t}^{2}}\]
\[[{{v}^{2}}={{u}^{2}}+2as]\]
In scalar product form \[\overrightarrow{v.}\overrightarrow{v}=\overrightarrow{u}.\overrightarrow{u}=2\overrightarrow{a}.\overrightarrow{s}\]
Accelerated Motion
\[[{{S}_{n}}th=u+\frac{a}{2}(2n-1)]\]
MOTION UNDER GRAVITY (FREE FALL)
The most important example of motion in a straight line with constant acceleration is motion under gravity. In case of motion under gravity,
(i) the acceleration is constant,
(a) the motion is in vacuum, so viscous force or thrust of the medium has no effect on the motion.
(1) Body falling freely under gravity: Taking initial position as origin and downward direction of motion as positive, we have
u=0 [as body starts from rest]
a = +g [as ace. is in the direction of motion]
So if the body acquires velocity v after falling a distance h in time t, equations of motion, viz:
\[v=u+at\,\,;\,\,s=ut+\frac{1}{2}\,\,a{{t}^{2}}\] and \[{{v}^{2}}={{u}^{2}}+2as\]
reduces to \[v=gt\] … (1)
\[h=\frac{1}{2}\,\,g{{t}^{2}}\] … (2)
\[{{v}^{2}}=2gh\] … (3)
These equations can be used to solve most of the problems of freely falling body.
(i) If the body is dropped from a height H, as in time t, it has fallen a distance h from its initial position, the height of the body from the ground will be
\[h'=H-h\]with h=\[\frac{1}{2}g{{t}^{2}}\]
(ii)\[As\,\,h=\frac{1}{2}\,\,g{{t}^{2}},\,\,i.e.,\,\,h\,\,\alpha \,\,{{t}^{2}}\]
So distance covered by a body fallen in time t, 2t, 3t
etc., will be in the ratio of \[{{1}^{2}}:{{2}^{2}}:{{3}^{2}},\,\,i.e.\] i.e., square of integers.
(ii) The distance covered by a body fallen in the \[{{n}^{th}}\] sec
\[={{h}_{(n)}}-{{h}_{(n-1)}}=\frac{1}{2}\,\,g\,\,{{(n)}^{2}}-\frac{1}{2}\,\,g\,\,{{(n-1)}^{2}}=\frac{1}{2}\,\,g\,\,(2n-1)\]
So distances fallen in Ist, 2nd, 3rd sec etc. will be in the ratio of 1 : 3 : 5 i.e., odd integers only.
(2) Body projected vertically up: Taking initial position as origin and direction of motion (i.e., vertically up) as positive, here we have v=0 [at highest point velocity = 0]
\[\therefore \] \[a=-g\][as ace. is downwards while motion upwards]
Motion Under Gravity in Presence of Air Resistance
An object is thrown with speed u in upward direction during its motion it experiences constant air resistance R in the direction opposite to its motion.
Motion in upward direction: Total force during upward motion =mg+R
Hence, total acceleration, \[a=g+\frac{R}{m}\]
Time in upward motion, \[t=\frac{u}{g+\frac{R}{m}}\]
Maximum height, h\[=\frac{{{u}^{2}}}{2\left( g+\frac{R}{m} \right)}\]
RELATIVE VELOCITY
Relative velocity of an object A with respect to another object B, when both are in motion is the time rate at which object A changes its position with respect to object B.
If \[{{\overrightarrow{v}}_{A}}\]and \[{{\overrightarrow{v}}_{B}}\]be the respective velocities of object A and then relative velocity of A w.r.t. B is
\[{{\overrightarrow{v}}_{AB}}={{\overrightarrow{v}}_{A}}-{{\overrightarrow{v}}_{B}}\]
Similarly, relative velocity of B w. r. t. A is
\[{{\overrightarrow{v}}_{BA}}={{\overrightarrow{v}}_{B}}-{{\overrightarrow{v}}_{A}}\]
Special Cases
(a) When the two objects move with equal velocities
i.e., \[{{v}_{A}}={{v}_{B}}\,\,\,or\,\,{{v}_{B}}-{{v}_{A}}=0\]
(b) When the two objects move with unequal velocities
(i) When\[{{v}_{A}}>{{v}_{B}}\], then \[{{v}_{B}}-{{v}_{A}}\]is negative.
(ii) When\[{{v}_{B}}>{{v}_{A}}\], then\[{{v}_{B}}-{{v}_{A}}\] is positive.
(c) When two trains A and B move with same velocity v but in opposite direction
The relative velocity of train A w.r.t. train B
\[{{\overrightarrow{v}}_{AB}}={{\overrightarrow{v}}_{A}}-{{\overrightarrow{v}}_{B}}=v(\hat{i})-v(-\overrightarrow{i})=2v(\hat{i})\]
Relative velocity of train B w.r.t. A
\[{{\overrightarrow{v}}_{BA}}={{\overrightarrow{v}}_{B}}-{{\overrightarrow{v}}_{A}}=v(-\hat{i})-v(i)=2v(-i)\]
(d) When the two bodies moving in directions inclined to each other
The magnitude of the relative velocity \[{{v}_{AB}}\]is given by
\[{{v}_{AB}}=\sqrt{{{v}_{A}}^{2}+{{v}_{B}}^{2}+2{{v}_{A}}{{v}_{B}}\cos (180{}^\circ -\theta )}\]
\[=\sqrt{{{v}_{A}}^{2}+{{v}_{B}}^{2}-2{{v}_{A}}{{v}_{B}}\cos \theta }\]
Let \[\alpha \] be the angle made by \[{{v}_{AB}}\] with \[{{v}_{A}},\]then
tan\[\alpha \]\[=\frac{{{v}_{B}}\sin (180{}^\circ -\theta )}{{{v}_{A}}+{{v}_{B}}\cos (180{}^\circ -\theta )}=\frac{{{v}_{B}}\sin \theta }{{{v}_{A}}-{{v}_{B}}\cos \theta }\]
\[or\,\,\alpha ={{\tan }^{-1}}\left( \frac{{{v}_{B}}\sin \theta }{{{v}_{A}}-{{v}_{B}}\cos \theta } \right)\]
\[\angle \alpha \]gives the direction of the relative velocity with \[\overrightarrow{v}\,\,A\]
Note:
When two bodies move in opposite directions, the magnitude of relative velocity of one with respect to the other is equal to the sum of the magnitudes of two velocities.
Relative Velocity of Rain w.r.t. the Moving Man
A man walking west with velocity\[{{\overrightarrow{v}}_{m}}\], represented by \[\overrightarrow{OA}\]Let the rain be falling vertically downwards with velocity \[{{\overrightarrow{v}}_{r}},\] represented by \[\overrightarrow{OB}\]as shown in fig.
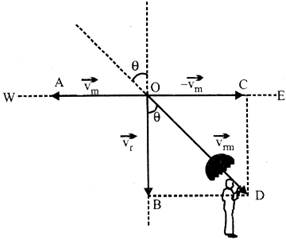
The relative velocity of rain w.r.t. man \[{{\overrightarrow{v}}_{rm}}={{\overrightarrow{v}}_{r}}-{{\overrightarrow{v}}_{m}},\] will be presented by diagonal\[\overrightarrow{OD}\]of rectangle OBDC.
\[\therefore \,\,\,{{\overline{v}}_{rm}}=\sqrt{{{v}^{2}}_{r}+{{v}^{2}}_{m}+2{{v}_{r}}{{v}_{m}}\cos 90{}^\circ }=\sqrt{{{v}_{r}}^{2}+{{v}_{m}}^{2}}\]
If\[\theta \]is the angle which \[{{\overrightarrow{v}}_{rm}}\] makes with the vertical direction.
Then, \[\tan \theta =\frac{BD}{OB}=\frac{{{v}_{m}}}{{{v}_{r}}}\,\,or\,\,\theta ={{\tan }^{-1}}\left( \frac{{{v}_{m}}}{{{v}_{r}}} \right)\]
Here angle \[\theta \] is from vertical towards west and is written as \[\theta \] west of vertical.
Note:
In the above case if the man wants to protect himself from the rain, he should hold his umbrella in the direction of relative velocity of rain w.r.t. man i.e. the umbrella should be hold making
An angle \[\left( \theta ={{\tan }^{-1}}\frac{{{v}_{m}}}{{{v}_{r}}} \right)\]west of vertical
River-Boat Problems
Minimum distance of approach
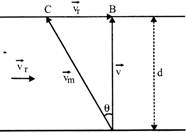
Let d = width of river, \[{{v}_{r}}\]= velocity of river water,
\[{{v}_{m}}\]= velocity of swimmer
->
The swimmer should swim in a direction such that resultant \[\overrightarrow{v}\] of \[{{\overrightarrow{v}}_{m}}\] and \[{{\overrightarrow{v}}_{r}}\]is along AB which is the shortest path.
\[\sin \theta =\frac{{{v}_{r}}}{{{v}_{m}}};\,\,\,\,\,v=\sqrt{{{v}_{m}}^{2}-{{v}_{r}}^{2}};\,\,\,t=\frac{d}{\sqrt{{{v}_{m}}^{2}-{{v}_{r}}^{2}}}\]
\[or,\,\,d=-\sqrt{{{v}_{m}}^{2}-{{v}_{r}}^{2}t}\]
Minimum time of approach
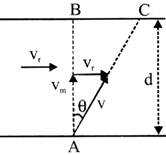
Time of crossing the river t \[=\frac{d}{{{v}_{m}}\cos \theta }\]
\[t={{t}_{\min }}when\,\,\cos \theta =+1=\cos 0{}^\circ \,\,\,i.e.\theta =0{}^\circ \]
\[{{t}_{\min }}=\frac{d}{{{v}_{m}}}\]
To cross the river in shortest time man should swim perpendicular to direction of flow.
Man will reach C instead of B
If BC=x then, \[\tan \theta =\frac{{{v}_{r}}}{{{v}_{m}}}=\frac{x}{d}\]
so, \[x=\frac{{{v}_{r}}}{{{v}_{m}}}.d\]
You need to login to perform this action.
You will be redirected in
3 sec
