JEE Main & Advanced Mathematics Definite Integration Volumes and Surfaces of Solids of Revolution

If a plane curve is revolved about some axis in the plane of the curve, then the body so generated is known as solid of revolution. The surface generated by the perimeter of the curve is known as surface of revolution and the volume generated by the area is called volume of revolution.

For example, a right angled triangle when revolved about one of its sides (forming the right angle) generates a right circular cones.

(1) Volumes of solids of revolution

(i) The volume of the solid generated by the revolution, about the x-axis, of the area bounded by the curve \[y=f(x),\]  the ordinates at \[x=a,\,x=b\] and the x-axis is equal to \[\pi \int_{a}^{b}{{{y}^{2\,}}\,dx}\].       

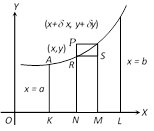
(ii) The revolution of the area lying between the curve \[x=f(y)\] the y-axis and the lines \[y=a\] and \[y=b\] is given by (interchanging \[x\] and \[y\] in the above formulae) \[\int_{a}^{b}{\pi \,{{x}^{2\,}}}\,dy\].

(iii) If the equation of the generating curve be given by \[x={{f}_{1}}(t)\] and \[y={{f}_{2}}(t)\] and it is revolved about x-axis, then the formula corresponding to \[\int_{a}^{b}{\pi \,{{y}^{2\,}}\,dx}\] becomes \[\int_{{{t}_{1}}}^{{{t}_{2}}}{\pi {{\{{{f}_{2}}(t)\}}^{2}}\,d\,\{{{f}_{1}}(t)\}}\],

where \[{{f}_{1}}\] and \[{{f}_{2}}\] are the values of t corresponding to \[x=a\]  and  \[x=b\].

(2) Area of surfaces of revolution

(i) The curved surface of the solid generated by the revolution, about the x-axis, of the area bounded by the curve \[y=f(x)\], the ordinates at \[x=a,\,\,x=b\] and the x-axis is equal to \[2\pi \int_{x=a}^{x=b}{\,\,\,y\,ds}\].

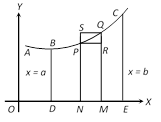
(ii) If the arc of the curve \[y=f(x)\] revolves about y-axis, then the area of the surface of revolution (between proper limits) \[=2\pi \int_{{}}^{{}}{x\,ds,}\] where \[ds=\sqrt{1+{{\left( \frac{dy}{dx} \right)}^{2}}}\,dx\].

(iii) If the equation of the curve is given in the parametric form \[x={{f}_{1}}(t)\] and \[y={{f}_{2}}(t)\], and the curve revolves about x-axis, then we get the area of the surface of revolution\[=2\pi \int_{t={{t}_{1}}}^{t={{t}_{2}}}{yds\,}\]

\[=2\pi \int_{t={{t}_{1}}}^{t={{t}_{2}}}{\,{{f}_{2}}(t)ds}\]\[=2\pi \int_{{{t}_{1}}}^{{{t}_{2}}}{{{f}_{2}}(t)\sqrt{\left\{ {{\left( \frac{dx}{dt} \right)}^{2}}+{{\left( \frac{dy}{dt} \right)}^{2}} \right\}}\,dt}\],

where \[{{t}_{1}}\] and \[{{t}_{2}}\] are the values of the parameter corresponding to \[x=a\] and \[x=b\].

(3) Volume and surface of the frustum of a cone : If \[{{r}_{1}},\,{{r}_{2}}\] be the radii of the circular ends and k is the distance between centres of circular ends and l be the slant height, then

(i) Volume of frustum of cone \[=\frac{\pi k}{3}(r_{1}^{2}+{{r}_{1}}{{r}_{2}}+r_{2}^{2})\]

(ii) Curved surface area of frustum of cone \[=\pi ({{r}_{1}}+{{r}_{2}})\,l\]

(iii) Whole surface area of frustum of cone

\[=\pi ({{r}_{1}}+{{r}_{2}})\,l\,+\pi \,r_{1}^{2}+\pi r_{2}^{2}\].

(4) Volume and surface of the frustum of a sphere : Let the thickness of the frustum of sphere is k and radii of the circular ends of the frustum are \[{{r}_{1}}\] and \[{{r}_{2}}\], then

(i) Volume of the frustum of sphere \[=\frac{\pi k}{6}(3r_{1}^{2}+3r_{2}^{2}+{{k}^{2}})\]

(ii) Curved surface area of frustum of sphere \[=2\pi ak\] (where \[a\] is radius of circle)

(iii) Whole surface area of frustum of sphere

\[=(2\pi ak+\pi r_{1}^{2}+\pi r_{2}^{2})\].