9th Class Mathematics Related to Competitive Exam Mensuration

Mensuration

Category : 9th Class

MENSURATION

Learning Objectives

Introduction
Area of Plane Geometrical Figures
Quadrilateral
Solids

Introduction

Mensuration is a science of measurement of the lengths of lines, area of surfaces and volumes of solids.

Some Important Definitions and Formulae:

If any closed figure has three sides then it is called a triangle.
In a triangle the sum of three angles is \[180{}^\circ \].
In a triangle the sum of the lengths of any two sides should be more than the third side.
Similarly the difference between any two sides of a triangle is less than the third side.
The side on which a triangle rests is called the base. The length of the perpendicular drawn on the base from opposite vertex is called the height of the triangle.
If the three sides of a triangle have three different lengths then it is called a scalene triangle.
If exactly two side of a triangle are equal and the third side has different length then it is called an isosceles triangle.
If all the three sides of a triangle are equal then it is called an equilateral triangle.

Area of Plane Geometrical Figures

Triangle

(i) Right Triangle

(ii) Scalene Triangle (Heron's formula)

(iii) Isosceles Triangle

(iv) Equilateral Triangle

Right Triangle: Area of right triangle \[=\frac{1}{2}\times \left( perpendicular \right)\times Base=\frac{1}{2}\times AB\,\times BC\]

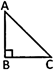
Scalene Triangle (Heron's formula): Let, a, b, c be the length of sides of a triangle

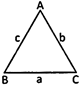
then area \[=\sqrt{s(s-a)(s-b)(s-c)}\] sq. unit, where \[s=\frac{1}{2}(a+b+c)\]

Isosceles Triangle: Area ot isosceies trsang Se

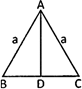
\[=\frac{1}{2}\times BC\times AD=\frac{1b}{4}\sqrt{4{{a}^{2}}-{{b}^{2}}}\]

Equilateral triangle:

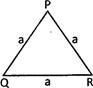
Area \[=\frac{\sqrt{3}}{4}\,{{(side)}^{2}}=\frac{\sqrt{3}}{4}{{a}^{2}}\]

Circle

A circle is a geometrical figure consisting of all those points in a plane which are at a given distance from a fixed point in the same plane. The fixed point is called the centre and the constant distance is known as the radius.

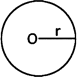
A circle with centre O and radius r is generally denoted by C (0, r).

Circle Formulas

The circumference C of a circle of radius r is given by the formula \[C=2{}^\circ \,\pi r\].
The area A of a circle of radius r is given by the formula \[A=\pi {{r}^{2}}\].
The areas of two circles are to each other as the squares of their radii.
The length L of an arc of \[n{}^\circ \] in a circle of radius r is given by the formula \[L=\frac{n}{360}\times 2\pi r\]
The area A of a sector of a circle of radius r with central angle of \[n{}^\circ \] is given by \[A=\frac{n}{360}\times \pi {{r}^{2}}\]

Quadrilateral

We know that a geometrical figure bounded by four lines segment is called quadrilateral In this section we will study about area and perimetre of different quadrilaterals.

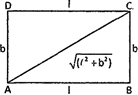
Rectangle

(i) Area \[=(l\,\times b)\]square units

(ii) Length \[=\frac{area}{breadth},\] breadth \[=\frac{area}{length},\]

(iii) \[\operatorname{Diagonal}\,=\sqrt{{{l}^{2}}+{{b}^{2}}}\,units\]

(iv) Perimetre \[=2(l+b)\]units

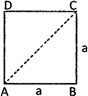
Square

Let ABCD be a square with each side equal to 'a' units then we have

(i) Area \[={{a}^{2}}\] sq units

(ii) Area \[=\left\{ \frac{1}{2}\times {{(diagonal)}^{2}} \right\}\] units

(iii) Diagonal \[=a\sqrt{2}\] units

(iv) Perimetre = 4a units

Area of parallelogram \[~= base\,\times height\]
Area of a Rhombus \[=\frac{1}{2}\times (product\,\,of\,diagonals\,)\]
Area of a Trapezium \[=\frac{1}{2}\left( Sum of parallel sides \right)\times \left( distance between them \right)\]

Solids

The objects having definite shape and size are called solids. A solid occupies a definite space.

Cuboid

Solids like matchbox, chalk box, a tile, a book an almirah, a room etc. are in the shape of a cuboid.

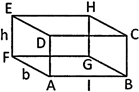
For cuboid of length = I, breath = b and height = h, we have:

(i) Volume \[=\left( I\,\times b\,\times h \right)\]

(ii) Total surface area \[=2 \left( Ib\,\times bh\,\times Ih \right)\]

(iii) Lateral surface area \[=\left[ 2(l+b)\times h \right]\]

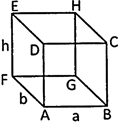
Cube

Solids like ice cubes, sugar cubes, dice etc. are the shape of cube Formula for a cube having each edge = a units, we have:

(i) Volume \[={{a}^{3}}\]

(ii) Total surface area \[=6{{a}^{2}}\]

(iii) Lateral surface area \[=4{{a}^{2}}\]

Cylinder

Solids like measuring jar, circular pencils, circular pipes, road rollers, gas cylinders, are said to have a cylindrical shape. Formula for a cylinder of base radius = r & height (or length) = h, we have

(i) Volume \[=\pi {{r}^{2}}h\]

(ii) Curved surface area\[=2\pi rh\]

(iii) Total surface area \[=(2\pi rh\,+\,2\pi {{r}^{2}})=2\pi r(h+r)\]

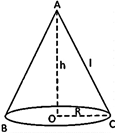
Cone

Consider a cone in which base radius = r, height = h & slant height \[\operatorname{l}=\sqrt{{{h}^{2}}+{{r}^{2}}}\] then we have

(i) Volume of the cone \[=\frac{1}{3}\pi {{r}^{2}}h\]

(ii) Curved surface area of the cone = (curved surface area) + (area of the base)

\[=\pi rl+\pi {{r}^{2}}=\pi r(l+r)\]

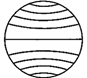
Sphere

Objects like a football, a cricket ball, etc. are said to have the shape of a sphere. For a sphere of radius r, we have

(i) Volume of the sphere \[=\left( \frac{4}{3}\pi {{r}^{3}} \right)\]

(ii) Surface area of the sphere \[=(4\pi {{r}^{2}})\]

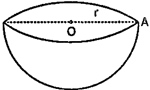
Hemisphere

A plane through the centre of a sphere cuts it into two equal parts, each part is called hemisphere.

For a hemisphere of radius r, we have:

(i) Volume of the hemisphere \[=\frac{2}{3}\pi {{r}^{2}}\]

(ii) Total surface area of the hemisphere \[=(2\pi {{r}^{2}})\]

(iii) Total surface area of the hemisphere \[=(3\pi {{r}^{2}})\]

Commonly Asked Questions

Find the area of a right - angle triangle with base 6 metres and hypotenuse 6»5 metres,,

(a) 7.1 sq. m. (b) 75 sq. m.

(e) None of these

Answer (b)

Explanation: Height \[=\sqrt{{{(6.5)}^{2}}-{{6}^{2}}}=\sqrt{(42.25-36)}=\sqrt{6.25}=2.5m\]

\[\therefore \,\,\,\,Area\,=\frac{1}{2}\times 6\times 2.5=7.2\,sq\,.m.\]

The perimeter of a rectangle is 640 meters and the length is to the breadth as 5 : 3, find its area.

(a) 24,000 sq. m. (b) 23,000 sq. m.

(e) None of these

Answer (a)

Explanation: Let length and breadth (in metres) respectively be 5X and 3x

\[2\left( 5x+3x \right)=640\]

\[16x=640\,\Rightarrow 40\]

\[\therefore \,\,\,Area\,=\,5X\times 3X=15{{x}^{2}}=15{{(40)}^{2}}=24,000\,sq.\,m.\,\]

What is the area of a square whose diagonal is 15 metres?

(a) 110. 5sq. m (b) 111. 4sq. m

(e) None of these

Answer: (c)

Explanation: Area of sq. \[=\,\frac{1}{2}\times {{(15)}^{2}}=112.5\,sq.m\]

Find the area of a rhombus one side of which measures 10 cm and one diagonal 12 cm

(a) 95 sq. m (b) 96 sq. m

(e) None of these

Answer (b)

Explanation: Let ABCD be rhombus.

\[\angle AOB\] is a right angle

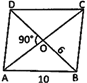
\[\operatorname{OB}=\frac{1}{2}(BD)\,=6cm,\,\,AB=10\,cm.\]

\[\Rightarrow AO 2 \left( AO \right)=16\,cm.\]

\[\therefore \,\,\,Area of rhombus =\frac{1}{2}\left( AC\times BD \right)=\frac{1}{2}\,\,\left( 16\times 12 \right)=96 sq. m.\]

The difference between the circumference and the diameter of a circle is 210 metres.

Find the radius of the circle.

(a) 49 m (b) 47 m

(e) None of these

Answer (a)

Explanation: If r be the radius,

\[2\pi r-2r=210\]

\[r=\frac{210}{2(\pi -1)}=\frac{105}{\frac{22}{7}-1}=\frac{7\times 105}{15}=49m.\]

The circumference of the base of a cylinder is 6 metres and its height is 44 metres. Find the volume.

(a) 124 cub. m (b) 123 cub. m

(e) None of these

Answer (d)

Explanation: If r be the radius of the base, \[2\pi r=6\]

\[r=\frac{3}{\pi }\]

\[\therefore \,\,\,Area\,\,of\,base\,=\pi {{r}^{2}}=p{{\left( \frac{3}{p} \right)}^{2}}=\frac{9}{\pi }\,sq.m.\]

\[\therefore \,\,\,Volume=\frac{9}{\pi }\,\times 44=\frac{9}{22}\times 7\times 44=126\,cub.m.\]

9th Class Mathematics Related to Competitive Exam Mensuration

Other Topics

Notes - Mensuration