Number Systems
Category : 9th Class
Number Systems
Note: A number of the form \[\frac{\mathbf{a}}{\mathbf{b}}\] is a fraction. So all are rational numbers. in the fraction, ‘a’ is called the numbers and ‘b’ is called the denominator. e.g. \[\frac{\mathbf{1}}{\mathbf{2}}\mathbf{- }\frac{\mathbf{2}}{\mathbf{3}}\mathbf{,}\frac{\mathbf{7}}{\mathbf{6}}\mathbf{,}\frac{\mat hbf{6}}{\mathbf{11}}\mathbf{,-}\frac{\mathbf{2}}{\mathbf{9}}\mathbf{,}....\]
(i) Zero is a rational number.
Note: 0 by 0 is undefined.
(ii) Every integer is a rational number.
(iii) A rational number, may or may not be an integer.
(iv) To write W distinct rational numbers between any two rational numbers 'a' and \['b'\],
we write\[a=\frac{{{P}_{1}}}{q}\] and\[b=\frac{{{P}_{2}}}{q}\] such that \[\left( {{P}_{2}}\text{ }- \text{ }{{P}_{1}} \right)\]is a positive integer greater than \['n'\],
(Here a < b); \[{{P}_{1}},{{P}_{2}}\]and q are integers\[(q\ne 0)\].
p- +1 p. + 2 Pi + n
A set of n rational numbers can be written as
\[\frac{{{P}_{1}}+1}{q},\frac{{{P}_{2}}+2}{q},......,\frac{{{P}_{1}}+n}{q}\]
i.e.,\[a=\frac{{{p}_{1}}}{q}<\frac{{{p}_{1}}+1}{q}<\frac{{{p}_{1}}+2}{q}.....<\frac{{{p}_{1}}+ n}{q}<\frac{{{p}_{2}}}{q}=b\]
Between two given rational numbers a and b, there are infinitely many rational numbers.
(i) If \[\frac{p}{q}\], is a rational number and \['m'\] is a non-zero integer, then \[\frac{p}{q}=\frac{p\times m}{q\times m}\]
(iii) Two rational numbers are equivalent only when the product of the numerator of the first rational number and the denominator of the second is equal to the product of the denominator of the first and the numerator of the second.
Note \[\frac{\mathbf{-p}}{\mathbf{q}}\mathbf{=}\frac{\mathbf{p}}{\mathbf{-q}}\mathbf{=- }\frac{\mathbf{p}}{\mathbf{q}}\]
(i) Rational numbers of the form \[\frac{m}{n}\] where m < n are represented on the number line as shown below.
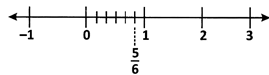
(ii) Rational numbers of the form \[\frac{m}{n}\] where m > n are represented on the number line as shown below.
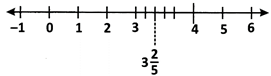
Note:\[\pi \] is an irrational number.
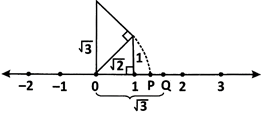
(i) The sum of two rational numbers is a rational number.
(ii) The sum of two irrational numbers may or may not be irrational.
(ii) The product of two rational numbers is a rational number,
(iv) The product of two irrational numbers may or may not be irrational.
(v) The difference of two rational numbers is a rational number.
(vi) The sum of a rational number and an irrational number is an irrational number.
(vii) The difference of a rational number and an irrational number is an irrational number.
(viii) The product of a rational number and an irrational number is an irrational number.
(ix) The quotient of two rational numbers is a rational number.
\[\operatorname{Exception}:\frac{\operatorname{Any} rational number}{0}=\infty \] (x) The quotient of two irrational numbers may or may not be irrational.
(xi) The quotient of a rational number and an irrational number is an irrational number.
\[\operatorname{Exception}:\frac{0}{\operatorname{Any} rational number}=\infty \]
Definition: A number whose square is non-negative is called a real number.
Note: (i) Every point on the number line, represents either a rational number or an irrational number i.e., a real number.
(ii) Corresponding to every point on the number line. There is a unique real number. And Corresponding to every real number, there is a unique point on the number line.
(i) Every rational number\[\frac{p}{q}\left( p,q\in Z\,\operatorname{and}\,q\ne 0 \right)\] can be expressed in the form of terminating or non- terminating recurring decimal.
(ii) Every irrational number can be expressed as a non-terminating non-recurring decimal.
Square root of a given positive real number: Let \['a'\] be any positive real number. We can express \[\sqrt{a=b}\] if and only if b > 0 and \[{{b}^{2}}\]= a. The value of \['b'\]is called the positive square root of the positive real number 'a'.
(i) \[{{\left( \sqrt{\operatorname{x}} \right)}^{2}}=\operatorname{x}\]) Where x is a positive real number.
(ii)\[\sqrt{\operatorname{x}}\times \sqrt{\operatorname{y}}=\sqrt{\operatorname{xy}}\] Where x and y are positive real numbers.
(iii) \[\frac{\sqrt{\operatorname{x}}}{\sqrt{\operatorname{y}}}=\sqrt{\frac{\operatorname{x}}{\operatorna me{y}}}\]where x and y are positive real numbers.
(v)\[{{\left( \sqrt{\operatorname{x}}+\sqrt{\operatorname{y}} \right)}^{2}}=\operatorname{x}+y+2\sqrt{\operatorname{xy}}\,\operatorname{and}{{\left( \sqrt{\operatorname{x}}-\sqrt{\operatorname{y}} \right)}^{2}}=x+y-2\sqrt{xy}\] Where x and y are positive real numbers.
(vi)
\[(\sqrt{a}+\sqrt{b})\times (\sqrt{\operatorname{c}}+\sqrt{d})=\sqrt{ac}+\sqrt{ad}+\sqrt{bc}+\sqrt{bd}\]where a, b, c and d are positive real numbers.
where 'a' is any real number and 'b' is a positive real number.
(i) The rationalizing factor of\[\frac{a}{\sqrt{\operatorname{x}}}\operatorname{is}\sqrt{\operatorname{x}}\].
(ii) The rationalizing factor of\[\frac{1}{a+b\sqrt{x}}\,\operatorname{is}\,\,\operatorname{a}-b\sqrt{x}\].
(iii) The rationalizing factor of \[\frac{1}{a\sqrt{\operatorname{x}}+b\sqrt{\operatorname{y}}}\,\operatorname{is}\,\,\operatorname{a }\sqrt{x}-b\sqrt{\operatorname{y}}\]
(iv)The rationalizing factor of\[\frac{1}{a-b\sqrt{\operatorname{x}}}\operatorname{is}\left( a+b\sqrt{\operatorname{x}} \right)\].
(v) The rationalizing factor of\[\frac{1}{a\sqrt{\operatorname{x}}- b\sqrt{\operatorname{y}}}\operatorname{is}\,\operatorname{a}\sqrt{x}+b\sqrt{y}\].
(positive integer), then\[{{a}^{n}}=a\times a\times ........\times a\](\['n'\] factors). Here, (\[{{a}^{n}}\]) is called the \[{{n}^{th}}\]power of a. The real number 'a' is called the base and positive integer 'n' is called the exponent.
For any rational base a; and any integers 'm' and 'n', we have
(i)\[{{a}^{m}}\times {{a}^{n}}={{a}^{m+n}}\] (ii) \[{{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}\]
(iii) \[\frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m-n}};m>n\] (iv) \[{{a}^{n}}\times {{b}^{n}}={{\left( a\times b \right)}^{n}}\]
(v) \[\frac{{{a}^{n}}}{{{b}^{n}}}=\left( \frac{{{a}^{n}}}{{{b}^{n}}} \right);b\ne 0\] (vi) \[\frac{{{a}^{n}}}{{{b}^{n}}}=\left( \frac{{{a}^{n}}}{{{b}^{n}}} \right);b\ne 0\]
(vii) \[{{a}^{o}}=1\] (viii) \[\frac{1}{{{a}^{n}}}={{a}^{-n}}\]
(ix) \[{{a}^{-n}}=\frac{1}{{{a}^{n}}}={{\left( \frac{1}{a} \right)}^{n}}\]
Note: For any positive real number a
Overall view of the number system:
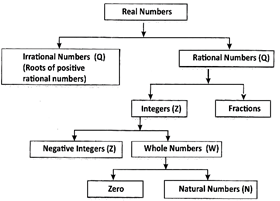
You need to login to perform this action.
You will be redirected in
3 sec
