9th Class Mathematics Lines and Angles

Lines and Angles

• Angle: An angle is the union of two rays with a common initial point. An angle is denoted by symbol\[\angle \]. It is measured in degrees,

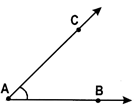
The angle formed by the two rays \[\overline{AB}\,\,and\,\,\overline{AC}\text{ }is\text{ }\angle BAC\text{ }or\text{ }\angle CAB.~\]called \[\overline{AB}\,\,and\,\,\overline{AC}\]are called the arms and the common initial point ‘A’ is called the vertex of the angle.  

• Bisector of an angle: A line which divides an angle into two equal a parts is alled the bisector of the angle.

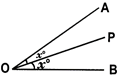
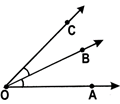
e.g., In the adjacent figure, the line OP divides \[\angle \]AOB into two       

Equal parts.

            \[\angle AOP=\angle POB={{\operatorname{x}}^{o}}\]                                         

So, the line OP is ‘called the bisector of \[\angle \]AOB.

• Pairs of angles:

(i) Complementary angles: Two angles are said to be Complementary if the sum of their measures is equal to\[~{{90}^{o}}\]

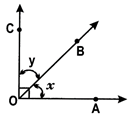
Here\[\angle x+\angle y={{90}^{o}},\]therefore \[\angle x\,\operatorname{and}\,\angle y\] Complementary angles:

(ii)  Supplementary angles: Two angles are said to be supplementary if the sum of their measures isequal to\[{{180}^{o}}\].

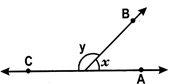
Here \[\angle x+\angle y={{180}^{o}},\]therefore \[\angle x\,\operatorname{and}\,\angle y\]

Supplementary angles.

• Adjacent angles: Angles having the same vertex and a common arm, and the non-common arms lie on the opposite sides of the common arm are called adjacent angles.

• \[\angle AOB\text{ }and\text{ }\angle COB\]with common vertex 0 and common arm OB are adjacent angles,

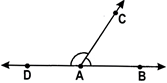
Note: \[\angle AOC=\angle AOB+\angle BOC\]

• Linear pair of angles: Two adjacent angles make a linear pair of angles, if the non-common arms of these angles are two opposite rays (with same end point),

• In the adjacent figure, \[\angle BAC\text{ }and\text{ }\angle CAD\]form a linear pair of angles because the non -common arms AB and AD of the two angles are two opposite rays.

Moreover,\[\angle \text{ }BAC\text{ }+\text{ }\angle DAC={{180}^{o}}\]

Note: Linear pair of angles \[\xrightarrow[\mathbf{always}]{\mathbf{are}}\]Adjacent angles.

Adjacent angles \[\xrightarrow[\mathbf{always}]{\mathbf{are}\,\,\mathbf{not}}\] Linear pair angles.

(ii) Linear pair of angles are supplementary.

• Vertically opposite angles: Two angles having the same vertex are said to form a pair of vertically opposite angles, if their arms form two pairs of opposite rays.

In the above figure,\[\angle BOD\text{ }and\text{ }\angle AOC\] is a pair of vertically opposite angles because they have a common vertex and also OB, OA; OC, OD are two pairs of opposite rays.

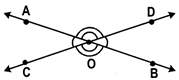
Similarly, we find that \[\angle BOD\text{ }and\text{ }\angle AOC\]is a pair of vertically opposite angles because they have common vertex at 0 and also OB, OA; OC; OD are two pairs of opposite rays.

Note: If two lines intersect each other’s, the vertically opposite angles are equal.

Transversal: A line intersecting two or more distinct lines at distinct points is called a transversal.

In the adjacent figure, transversal EF intersects lines AB and CD at points P and Q respectively.       
     

• Here \[\angle 1,\angle 2,\text{ }\angle 7\text{ }and\text{ }\angle 8\]are called exterior angles whereas,\[\angle 3,\angle 4,\text{ }\angle 5\text{ }and\text{ }\angle 6\] are called interior angles.

• Corresponding angles: Two angles are said to be a pair of corresponding angles if they are on the same side of the transversal with one angle interior and the other angle exterior and

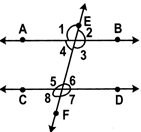
the angles are not adjacent angles. In the above figure, the pairs of corresponding angles are:

• (i) \[\angle 1\text{ }and\text{ }\angle 5\] (ii)\[\angle 2\text{ }and\text{ }\angle 6\]  

(iii)\[\angle \]3 and\[\angle \]7 and (iv) \[\angle \]4 and \[\angle \]8

• Co-interior angles or interior angles on the same side of the transversal: Two angles are

said to beco-ihterior angles if they are interior angles and lie on the same side of the

transversal. In the above figure, the pairs of co-interior angles are:

(i) \[\angle \]3 and \[\angle \]6 and     (ii)\[\angle \]4 and \[\angle \]5  

• Alternate angles: Two angles are said to be a pair of alternate angles if the angles are interior angles, which lie on either side of the transversal and are not adjacent angles.

• In the above figure, the pairs of alternate angles are:

(i) \[\angle \]4 and \[\angle \]6 and    (ii) \[\angle \]3 and \[\angle \]5

• Properties of corresponding angles: If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.

• Converse: If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.

• Properties of alternate angles:

(i) If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.

(ii) Converse: If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.

• Properties of co-interior angles:

If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal (i.e., co-interior angles) is supplementary.

• Converse: If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.

• Lines parallel to a given line are parallel to each other. In other words, if /, m and n be three lines such that \[l\]\[\parallel \]m and \[l\]\[\parallel \] n. then m \[\parallel \] n.

• Angle sum property of a triangle:

The sum of the three angles of a triangle is 180°.

In AABC, ZA + ZB + ZC = 180°.

• In a right angled triangle, the sum of the two acute angles is\[\,{{90}^{o}}\].
• If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.

In\[\Delta ABC,\text{ }\angle ACD\text{ }=\angle BAC+\angle ABC\].

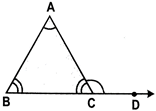
Note: An exterior angle of a triangle is greater than each of its interior angles.

In the above figure, \[\angle \]ACD is greater than \[\angle \]BAC as well as \[\angle \]ABC.