Introduction to Euclid's Geometry
Category : 9th Class
Introduction to Euclid's Geometry
- Axioms: Axioms or postulates are the assumptions which are obvious universal truths and are not to be proved.
- Some of the axioms given by Euclid: (i) Things which are equal to the same thing are equal to one another. i.e., if a = c and b = c, then a = b.
(ii) If equals are added to equals, the wholes are equal. i.e., if a = b and c = d, then a + c = b + d.
Also a = b \[\Rightarrow \]a+c=b+c.
Here, a, b, c and d are same kind of things.
(iii) If equals are subtracted from equals, the remainders are equal.
(iv) The things which coincide with one another are equal to one another.
(v) The whole is greater than the part.
i.e., if a > b, then there exists 'c' such that a = b + c.
Here, 'b' is a part of 'a' and therefore, 'a' is greater than 'b'.
(vi) Things which are double the same things are equal to one another.
- (vii) Things which are halves of the same things are equal to one another.
- Euclid's five postulates:
(i) Postulate 1: A straight line may be drawn from any one point to any other point.
(ii) Postulate 2: A terminated line (i.e., a line segment) can be produced indefinitely on either side to form a line.
(iii) Postulate 3: A circle can be drawn with any centre and any radius.
(vi) Postulate 4: All right angles are equal to one another,
(v) Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced a indefinitely, meet on that side on which the sum of angles is less than two right angles.
- Theorems or propositions are the properties which are to be proved, using definitions, axioms/postulates, previously proved statements and deductive reasoning.
- Any two distinct straight lines are either intersecting or parallel. If the two lines are intersecting, then they can be oblique to each other or perpendicular to each other.
- Intersecting lines: Two distinct straight lines which meet each other at a point are called intersecting straight lines.
- Perpendicular lines: Two intersecting lines are perpendicular to each other if one meets the other at a point and the angles made by the first with either side of the second at the point are each equal to one right angle.
- Parallel lines: Two distinct lines which are not intersecting are called parallel lines.
- Axioms of points and lines:
(i) Axiom 1: A line contains infinitely many points.
(ii) Axiom 2: Through a given point, infinitely many lines can be made to pass.
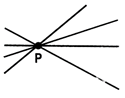
(iii) Axiom 3: Given two distinct points, there exists one and only one line passing through them.
- Collinear points: Three or more points are collinear if one and only one line can be made to pass through them.
- Concurrent lines: Three or more lines are said to be concurrent if they all pass through a
- Unique point. The point is called the point of concurrence of the lines.
- Two distinct lines cannot have more than one point in common.
- Play fair’s axiom: (Axiom for parallel lines): For every line /and for every point P not lying on /, there exists a unique line m passing through P and parallel to.
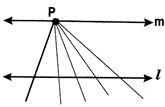
- Another version for the above axiom is stated as:
- Two distinct intersecting lines cannot be parallel to the same line.
- If a point C lies between two points A and B, then AC + BC = AB.
- If C is the midpoint of a line segment AB, then AC = BC = - AB.
- There is one and only one midpoint of a line segment.



