9th Class Mathematics Heron's Formula

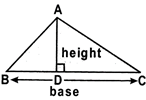
Heron's Formula

• Area of a triangle \[=\frac{1}{2}\times \operatorname{base}\,\times \,height\]

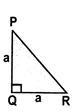
• Area of a right angled isosceles triangle with perpendicular sides each equal to 'a' units\[=\frac{1}{2}{{a}^{2}}\] sq. Units.

• Heron's formula:

            Area of a triangle \[=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}\]where a, b, c are the sides of the triangle and

            s = semi perimeter i.e., half the perimeter of the triangle =\[=\frac{a+b\text{ }+c}{2}\]

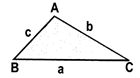
Note: Heron's formula can be used when three sides of triangle are given and can be applied to any triangle.                                                  

• Area of an equilateral triangle with each side equal to 'a' units \[=\frac{\sqrt{3}}{4}{{a}^{2}}\]sq. units.
• Area of an equilateral triangle\[=\frac{{{h}^{3}}}{\sqrt{3}}\]sq. units where altitude\[h=\frac{\sqrt{3}}{2}a\] units.
• Area of a quadrilateral whose sides and one diagonal are given, can be calculated by dividing the quadrilateral into two triangles and using the Heron's formula.

• Three positive integers a, b and c such that is\[{{c}^{2}}={{a}^{2}}+{{b}^{2}}\] called a Pythagorean triplet.