GEOMETRY
Learning Objectives
Geometry
Geometry is the visual study of shapes, sizes, patterns, and positions. It occurred in all cultures, through at least one of these five strands of human activities: The following formulas and relationships are important in solving geometry problems.
Angle Relationships
- The base angles of an isosceles triangle are equal.
- The sum of the measures of the interior angles of any n-sided polygon is 180 (n – 2) degrees.
- The sum of the measures of the exterior angles of any n-sided polygon is \[360{}^\circ \].
- If two parallel lines are cut by a transversal, the alternate interior angles are equal, and the corresponding angles are equal.
Angle Measurement Theorems
- A central angle of a circle is measured by its intercepted arc.
- An inscribed angle in a circle is measured by one-half of its intercepted arc.
- An angle formed by two chords intersecting within a circle is measured by one-half the sum of the opposite intercepted arcs.
- An angle formed by a tangent and a chord is measured by one-half its intercepted arc.
- An angle formed by two secants, or by two tangents, or by a tangent and a secant, is measured by one-half the difference of the intercepted arcs.
Proportion Relationships
- A line parallel to one side of triangle divides the other two sides proportionally.
- In two similar triangles, corresponding sides, medians, altitudes, and angle bisectors are proportional.
- If two chords intersect within a circle, the product of the segments of one is equal to the product of the segments of the other.
- If a tangent and a secant are drawn to a circle from an outside point, the tangent is the mean proportional between the secant and the external segment.
- In similar polygons the perimeters have the same ratio as any pair of corresponding sides.
Right Triangle Relationships
- If an altitude is drawn to the hypotenuse of a right triangle it is the mean proportional between the segments of the hypotenuse, and either leg is the mean proportional between the hypotenuse and the segment adjacent to that leg.
- In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. (Remember the Pythagorean triples: 3, 4, 5; 5, 12, 13.)
- En a \[30{}^\circ -60{}^\circ \] right triangle, the leg opposite the \[30{}^\circ \]angle is one-half the hypotenuse, and the leg opposite the \[60{}^\circ \] angle is one-half the hypotenuse times\[\sqrt{3}\].
- In a right isosceles triangle the hypotenuse is equal to either leg times. \[\sqrt{2}\].
- En an equilateral triangle of sides, the altitude equals \[\frac{s}{2}\sqrt{3}\].
Commonly Asked Questions
- If the sides of a triangle are produced then the sum of the exterior angles i.e,
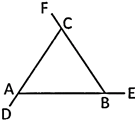
\[\angle DAB\,\,+\,\,\angle EBC\,\,+\,\,\angle FCA\] is equal to:
(a) \[180{}^\circ \] (b) \[270{}^\circ \]
(c) \[360{}^\circ \] (d) \[240{}^\circ \]
(e) None of these
Answer (c)
Explanation: Sum of exterior angles \[=360{}^\circ \]
- In a \[\angle ABC, \angle BAC\,>\,\,90{}^\circ ,\] then \[\angle ABC\] and \[\angle ACB\,\] must be:
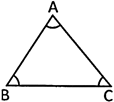
(a) acute
(b) obtuse
(c) one acute and one obtuse
(d) Can’t be determined
(e) None of these
Answer (a)
Explanation: \[\angle ABC+\angle ACB<90{}^\circ \]
- If the angles of a triangle are in the ratio \[1:4:7\]. the then the value of the largest angle is:
(a) \[135{}^\circ \] (b) \[84{}^\circ \]
(c) \[105{}^\circ \] (d)\[110{}^\circ \]
(e) None of these
Answer: (c)
Explanation: \[x+4x+7x=180{}^\circ \]
\[\Rightarrow x=15{}^\circ \]
\[\therefore 7x=150{}^\circ \]


