Circles
- A circle is a closed figure in a plane formed by
The collection of all the points in the plane which centre are at a constant distance from a fixed point in the plane. The fixed point is called the centre of length of radlus the circle and the constant distance is called the radius of the circle.
- The plane region inside the circle is called tne interior of the circle,
- If a circle is drawn in the plane X (infinite dimensions), then the part of the plane region outside the circular region is called the exterior of the circle.
- The circumference of a circle is the length of the complete circular curve constituting the circle, given by circumference, \[C=\text{2}\pi r\]where r is the radius of the circle.
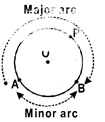
- Any two points A and B of a circle, divide the circle into two parts. The smaller part is called a minor arc of the circle denoted by \[\overset\frown{AB}\](read as arc AB).The larger part is called a major arc denoted by q\[\overset\frown{APB}\]or BA (read as arc\[\overset\frown{BA}\]).
- A line segment joining two points on the circumference of the circle, is called a chord of the circle. In the figure, AB is a chord.
- A chord passing through the centre O of the circle is called a diameter of the circle.
A diameter of a circle is the longest chord of the circle and its length is twice that of the radius of the circle. Diameter, d = 2r where r is the radius of the circle.
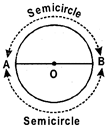
- A diameter of a circle divides it into two equal arcs. Each of these two arcs is called a semicircle. In the figure AB is a semicircle.
- A chord AB divides a circular region into two parts. The smaller part is called the minor segment and the larger part is called the major segment. In case chord AB is a diameter of the circle, the two segments are equal and each is called a semicircular region.
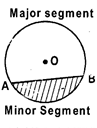
- Circles which have the same centre 0 and different radii OA (= r) and OB (= s) are called concentric circles.
- Two circles C (0, r) and C (0', s) are said to be congruent if and only if r=s.
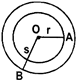
- One - fourth of a circle is called a quadrant. In the figure the shaded part is called a quadrant.
- The angle subtended by a chord AB at the centre 0 of a circle is\[\angle \]AOB.
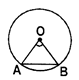
- The angle subtended by chord AB, at a point (the centre) is the same as the angle subtended by the arc AB at the same point (the centre).
- Equal chords of a circle subtend equal angles at the centre of the circle.
- Conversely, if two chords subtend equal angles at the centre of a circle. then the chords are equal.
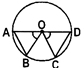
If \[AB=CD,\]then \[\angle AOB\text{ }=\angle COD.\]conversely, \[\angle AOB=\angle COD\,\]then AB = CD
Note: If two chords subtend angles of unequal measure at the centre of a circle, then the chords are unequal.
- The perpendicular drawn from the centre to a chord of the circle bisects the chord. Conversely, the line segment joining the centre of a circle to the mid-point of a chord of the circle the chord.
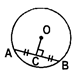
- If OC \[\bot \] AB, then AC = CB. Conversely, if AC = CB, then OC \[\bot \] AB.
- Equal chords of a circle are equidistant from the centre of the circle.
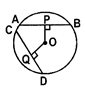
- Conversely, chords equidistant from the centre of a circle are equal.
- If AB = CD, then OP = OQ. Conversely, if OP = OQ, then AB = CD.
Note: Equal chords of congruent circles are equidistant from their respective centers. Conversely, chords equidistant from the corresponding centers of congruent circles are equal.
- One and only one circle can be made to pass through three given on- collinear points in a plane.
- If two chords of a circle are equal, then their corresponding arcs are congruent. Conversely, if two arcs are congruent, then their corresponding chords are equal.
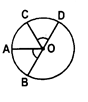
If AB = CD, then AB - CD. Conversiy. If \[\overset\frown{\operatorname{AB}}\]=\[\overset\frown{CD}\], then AB = C)
- Congruent arcs of a circle subtend equal angles at the centre of the circle.
If \[\overset\frown{\operatorname{AB}}=\overset\frown{CD},\text{ }then\,\angle AOB=\angle COD.\]the converse is also true.
The angle subtended by an arc at the centre is double the angle Subtended by it at any point on the remaining part of the circle.
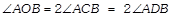
The angle subtended in a semicircle is a right angle.
\[\angle ACB\text{ }=\text{ }{{90}^{o}}\]
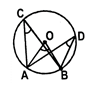
- Angles in the same segment of a circle are equal.
- If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle.
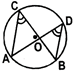
\[\angle ACB\text{ }and\text{ }\angle ADB\]are angles in the same segment.
\[\Rightarrow \]\[\angle ACB\text{ }and\text{ }\angle ADB\]
- If all the four vertices of a quadrilateral lie on a circle, then it is called a cyclic quadrilateral. ABCD is a cyclic quadrilateral. The sum of either pair of opposite angles of a cyclic quadrilateral is. In the figure,
\[\angle A\text{ }+\angle C={{180}^{o}}\,and\text{ }\angle B+\angle D\text{ }=\text{ }{{180}^{o}}\]. If the sum of a pair of opposite angles of a quadrilateral is 180°, then the quadrilateral is cyclic.
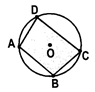
- A cyclic parallelogram is a rectangle.
- If one side of a cyclic quadrilateral is produced, then the exterior angle so formed is equal to the interior opposite angle.
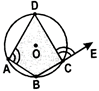
Here,\[\angle DCE=\angle DAB\].
- A line that touches a circle at a point is called a tangent. I is a tangent to the circle with centre 0. A is called the point of contact.
- A line segment that intersects a circle at two distinct points is called secant. \[\overleftrightarrow{AB}\]is the secant to the circle.












![]()



