Algebra
Category : 6th Class
ALGEBRA
ALGEBRA
The part of mathematics in which letters and other general symbols are used to represent numbers and quantities in formulae and equations.
Introduction to Algebra
Example: \[x,\,\,y,\,\,z\]etc.
Example: \[-1,\,\,\frac{1}{2},\,\,2,\,\,4,\,\,3,\,\,5\]etc.
Example: \[5{{x}^{2}},\,\,7x,\,\,\frac{x}{7},\,\,\frac{{{y}^{2}}}{9},\,\,\frac{5}{2}x\]etc.
Example: \[4,\,\,\frac{-1}{2},\,\,\frac{7}{4}\]etc.
Example: \[2a+3,\text{ }2a+3b,\text{ }7n+4,-p+-r+2\]etc.
Types of Algebraic Expressions;-
Example: \[7x,\,\,-11{{a}^{2}}{{b}^{2}},\,\,\frac{-7}{5}\]etc.
Example:\[2x+3,\text{ }6x-5y\] etc.
Example: \[2x+3y-\frac{5}{2},\frac{a}{2}-\frac{b}{3}+4\]etc.
Example:\[2x+3y-2,\text{ }7+6x+3y,\text{ }3\sqrt{x}+4\]etc.
Example: The degree of \[6{{x}^{2}}y\,\,{{z}^{3}}\]is\[2+1+3=6\]
Example: Degree of\[6{{x}^{2}}-5{{x}^{2}}2x-3\] is ' 3'. The degree of\[6{{x}^{6}}+5{{x}^{5}}\text{ }{{y}^{7}}+9\] is 12.
Example: \[x=1,\]is called a zero of\[x-1\].
Example:\[8{{x}^{2}}+2x+3,\] \[2p-3q+\frac{5}{2}r\]etc.
Example: \[15=3\times 5,\]where 3, 5 are called the factors of 15.
\[10xy=2\times 5\times x\times y,\]where\[2,\,\,5,\,\,x,\,\,y\]are called the factors of\[10\,\,xy\].
Example: In 6xy, 6 is called numerical coefficient of \['xy'\] and \['x'\] is the literal coefficient of \['7y'\] and \['y'\] is the literal coefficient of\[7x\].
Note: Degree of zero polynomial is not defined but some of the famous mathematicians claim the degree of zero polynomial is defined as \[-1\] or\[-\infty \].
Example: The value of \[9x\] at \[x=4\]is\[9\times 4=36\]
Operation of Algebraic Expression
Note: Unlike terms cannot be combined or added.
Example: \[2x+5x=7x,\,\,8xy+9xy=17xy\]etc.
Horizontal method
In this method, like terms should be added and unlike terms should be written separately by using associative law of addition.
Example: \[7x+4y\]and \[3x-5y\]
Solution: \[7x+4y+3x-5y\]
\[=7x+3x+4y-5y\]
\[=10x-y\]
Vertical method: following the steps.
Example:
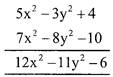
Subtraction of Algebraic Expressions:
The additive inverse of a number
The additive inverse of any number is obtained by a simple change of its sign, so additive inverse of a number is also called the negative of that number.
Example: Additive inverse of \[8\] is\[-8\].
Additive Inverse of Expression
Example: 1 Additive inverse of\[-~9x\]is\[9x\].
Example: 2 Subtract \[16x-5y\]from \[7x+4y\]
Solution: \[(7x+4y)-(16x-5y)\]
\[=7x+4y-16x+5y\]
\[=-9x+9y\]
Example: 3 Subtract \[3\times 2-5x-4\]from \[5{{x}^{2}}+6x+8\]
Solution: \[(5{{x}^{2}}+6x+8)-(3{{x}^{2}}-5x-4)\]additive inverse of \[\left( 3{{x}^{2}}-5x-4 \right)\]is \[-3{{x}^{2}}+5x-4\]
then, \[5{{x}^{2}}+6x+8-3{{x}^{2}}+5x-4\]
\[=\text{ }5{{x}^{2}}-3{{x}^{2}}+6x+5x+8-4\]
\[=2{{x}^{2}}+11x+4\]
Subtraction can also be done in two ways;
Example: \[\left( x+y \right)-\left( 2x+3y \right)\]
\[=x+y-2x-3y\]
\[=-x-2y\]
Example:
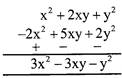
Multiplication of Algebraic Expression
\[{{a}^{m}}\times {{a}^{n}}={{a}^{m+n}}\] (a is any variable and m, n are positive integers.)
e.g. \[{{x}^{6}}\times {{x}^{7}}={{x}^{6+7}}={{x}^{13}}\]
Multiplication of monomials
Example: \[6xy\]and \[-3{{x}^{2}}y\]
Solution: \[(6xy)\times (-3{{x}^{2}}y)\]
\[=\{6\times -3\}\times ({{x}^{2}}y\times xy)\]
\[=-18{{x}^{3}}{{y}^{2}}\]
Multiplication of a Binomial and a monomial;
Example: \[2x\left( 3y+z \right)=2x\times 3y+2xz\]
\[=6xy+2xz\]
Multiplication can also done in two ways
Example: \[2x\left( 3x+5z \right)\]
\[=2x\times 3x+2x\times 5z\]
\[=6{{x}^{2}}+10xz\]
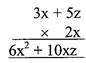
Multiplication of two binomials
\[\left( x+y \right)\times \left( a+b \right)=x\left( a+b \right)+y\left( a+b \right)\]
\[=\left( x\times a+x\times b \right)+\left( y\times a+y\times b \right)\]
\[=ax+bx+ay+by\]
Example: \[(3x-5y)\times (7x+4y)\]
\[=3x(7x+4y)-5y(7x+4y)\]
\[=(2x\times 7x+3x\times 4y)+(-5y\times 7x+4y\times -5y)\]
\[=21{{x}^{2}}+12xy-35xy-20{{y}^{2}}\]
\[=21{{x}^{2}}-23xy-20{{y}^{2}}\]
Division of Algebraic Expression
Example: Divide \[{{x}^{10}}\] by \[{{x}^{5}}\]
Solution: \[{{x}^{10}}\div {{x}^{5}}={{x}^{10-5}}={{x}^{5}}\]
Division of monomials
= (quotient of their numerical coefficients) \[\times \](quotient of their variables)
Example: \[~38{{x}^{2}}{{y}^{2}}\]by \[19xy\]
Solution: \[38{{x}^{2}}{{y}^{2}}\div 19xy\]
\[=\frac{38}{19}\times \frac{{{x}^{2}}{{y}^{2}}}{xy}\]
\[=2\times {{x}^{2-1}}.{{y}^{2-1}}\]
\[=2xy\]
Example: \[12{{x}^{4}}-6{{x}^{2}}+3x\] by \[3x\]
Solution: \[\left( 12{{x}^{4}}-6{{x}^{2}}+3x \right)\div 3x\]
\[=\frac{12{{x}^{4}}}{3x}-\frac{6{{x}^{2}}}{3x}+\frac{3x}{3x}\]
\[4{{x}^{3}}-2x+1\]
Division of a polynomial by a polynomial
Example: 1 \[\left( {{x}^{2}}+2x+1 \right)\] by \[\left( x+1 \right)\]
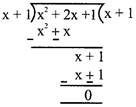
Example: 2 Divide \[{{x}^{3}}+8\]by \[x+2\]
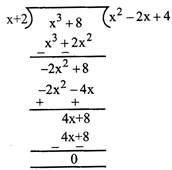
Special Products
(i) \[{{\left( a+b \right)}^{2}}+{{a}^{2}}+2ab+{{b}^{2}}\]
LHS \[={{\left( a+b \right)}^{2}}\]
\[=\left( a+b \right)\left( a+b \right)\]
\[=a\left( a+b \right)+b\left( a+b \right)\]
\[={{a}^{2}}+ab+ab+{{b}^{2}}\]
\[={{a}^{2}}+2ab+{{b}^{2}}\]
LHS = RHS
(ii) \[{{\left( a+b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\]
LHS \[=\left( a-b \right)\left( a-b \right)\]
\[=a\left( a-b \right)-b\left( a-b \right)\]
\[={{a}^{2}}-ab-ab+{{b}^{2}}\]
\[={{a}^{2}}-2ab+{{b}^{2}}\]
LHS = RHS
(iii) \[\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}\]
LHS \[=\left( a+b \right)\left( a-b \right)\]
\[=a\left( a-b \right)+b\left( a-b \right)\]
\[={{a}^{2}}-ab+ab-{{b}^{2}}\]
\[={{a}^{2}}-{{b}^{2}}\]
LHS = RHS
Example: 1 If \[x+\frac{1}{x}=5,\]find \[{{x}^{2}}+\frac{1}{{{x}^{2}}}\]
Solution: \[x+\frac{1}{x}=5\]
Squaring both sides
\[{{\left( x+\frac{1}{x} \right)}^{2}}={{\left( 5 \right)}^{2}}\]
\[={{x}^{2}}+\frac{1}{{{x}^{2}}}+2\times x\times \frac{1}{x}=25\]
\[={{x}^{2}}+\frac{1}{{{x}^{2}}}+2=25\]
\[={{x}^{2}}+\frac{1}{x}=25-2\]
\[\therefore \]\[{{x}^{2}}+\frac{1}{{{x}^{2}}}=23\]
Example: 2 Expand \[{{(x-3y)}^{2}}\]
Solution: \[\left( x-3y \right)\,\,\left( x-3y \right)\]
\[={{x}^{2}}-2\times 3y\times x+{{\left( 3y \right)}^{2}}\]
\[={{x}^{2}}-6xy+9{{y}^{2}}\]
Linear equation in one variable;
Equation:
LHS and RHS Notations
Example: \[7x+2=5x+3\]
Here, \[7x+2=\]LHS and \[5x+3=\]RHS
Linear Equation in one variable
Example: 1 \[4x-3=x+5\]
Example: 2 \[y+8=11\]
Solution of an Equation
Example: \[2x+10=4\]
Here, LHS \[=2x+10,\]RHS\[=14\]
Now, above equation is true only when \[x=2\]i.e. \[x=2\]
\[=LHS=2\times 2+10=14\]
\[RHS=14\]
\[\therefore \] LHS = RHS
\[\therefore \] Root of \[2x+10=14\] is 2.
Type of finding the solutions of linear equations
Example: (i) \[x+5=7\]
Solution: \[x=7-5\]
\[\therefore \]\[x=2\]
Example: (ii) \[\frac{x}{8}=5\]
Solution: \[x=5\times 8\]
\[x=40\]
Example: (iii) \[2x=40\]
Solution: \[2x40\]
\[x=\cancel{\frac{40}{2}}\]
\[\therefore \]\[x=20\]
Example: (iv) \[3x+2=x-2\]
Solution: \[2x=-4\]
\[x=\cancel{\frac{4}{2}}=-2\]
\[\therefore \]\[x=-2\]
Example: The sum of two numbers is 100 and their difference is 10. Find the numbers.
Solution: Let the numbers be\[x\], \[100-x\]
\[x-(100-x)=10\]
\[x-100+x=10\]
\[2x=110\]
\[x=55\]
Then the numbers are 55 and 45.
You need to login to perform this action.
You will be redirected in
3 sec
