Operation on Fractions
Category : 5th Class
Operation on Fractions
Operation on the Fractions
In the previous chapter, we have studied about the fractions. In this chapter we will study operations on the fractions, like addition, subtraction, multiplication and division on fractions.
Addition of Fractions
Make the denominator of fractions same by multiplying a suitable number to the numerator and denominator of both fractions. The common denominator is the denominator of the resultant fraction and addition of numerators is the numerator of the resultant fraction.
Example:
Add \[\frac{12}{16}\] and \[\frac{13}{16}\].
Solution: \[\frac{12}{16}+\frac{13}{16}=\frac{12+13}{16}=\frac{25}{16}\]
Add \[\frac{10}{9}\] and \[\frac{9}{10}\].
Solution: \[\frac{10}{9}=\frac{10}{9}\times \frac{10}{10}=\frac{100}{90}\]
\[\frac{9}{10}=\frac{9}{10}\times \frac{9}{9}=\frac{81}{90}\]
Therefore, their sum=
\[\frac{100}{90}+\frac{81}{90}=\frac{100+81}{90}=\frac{181}{90}\]
Subtraction of Fractions _
Make the denominator of each fraction same by multiplying a suitable number to the numerator and denominator of both fractions. The common denominator is the denominator of resultant fraction and result of numerators after subtraction is this numerator of the resultant fraction.
Subtract \[\frac{23}{27}\]from\[\frac{30}{27}\].
Solution: \[\frac{30}{27}-\frac{23}{27}=\frac{30-23}{27}=\frac{7}{27}\]
Subtract \[\frac{16}{17}\]from\[\frac{18}{19}\].
Solution: \[\frac{16}{17}\]=\[\frac{16\times 19}{17\times 19}=\frac{304}{323}\]
\[\frac{18}{19}\]= \[\frac{18\times 17}{19\times 17}=\frac{306}{323}\]
Therefore, difference = \[\frac{306}{323}-\frac{304}{323}=\frac{2}{323}\]
Multiplication of Fractions
Numerator is multiplied to numerator and denominator is multiplied to denominator on multiplication of any two fractions.
Find the product of \[\frac{13}{20}\] and \[\frac{6}{9}\].
Solution: \[\frac{13}{20}\times \frac{16}{19}=\frac{13\times 16}{20\times 19}=\frac{208}{380}\]
Find the product of \[\frac{23}{25}\] and \[\frac{175}{207}\].
Solution: \[\frac{23}{25}\times \frac{175}{207}=\frac{23\times 175}{25\times 207}=\frac{7}{9}\]
\[\{\because 23\times 9=207\text{ }and\text{ }25\times 7=175\}\]
Multiplication of a Fraction and a Whole Number
Simply, numerator of a fraction is multiplied by a whole number and denominator remains same as the denominator of a fraction.
Find the product of \[\frac{26}{15}\] and 22.
Solution: \[\frac{26}{15}\times 22=\frac{26\times 22}{15}=\frac{572}{15}\]
Find the product of 25 and \[\frac{127}{140}\].
Solution: \[25\times \frac{127}{140}=\frac{25\times 127}{140}=\frac{635}{28}\]
Division of Fractions
For division of fractions, we use following steps:
step1: Reverse the order of divisor fraction so that denominator becomes numerator and numerator becomes denominator and put the sign of multiplication in place of division.
step2: Multiply numerator by numerator and denominator by denominator.
Divide \[\frac{20}{33}\] by \[\frac{5}{11}\].
Solution:
\[\frac{20}{33}\div \frac{5}{11}=\frac{20}{33}\times \frac{11}{5}=\frac{4}{3}\]
Division of a Fraction by a Whole Number and Vice Versa
The steps used for division are:
Step1: Whole number is written as a fraction by taking 1 as denominator.
Step2: Reverse the order of divisor so that denominator becomes numerator and numerator becomes denominator, and put the sign of multiplication in place of division.
Step3: Multiply numerator with numerator and denominator with denominator.
Divide \[\frac{12}{15}\]by 25.
Solution:\[\frac{12}{15}\div 25=\frac{12}{15}\times \frac{1}{25}=\frac{12}{15\times 25}=\frac{4}{125}\]
Divide 216 by \[\frac{27}{36}\].
Solution:
\[216\div \frac{27}{36}=\]\[\frac{216}{1}\times \frac{36}{27}=\frac{216\times 36}{27}=24\times 12=288\]
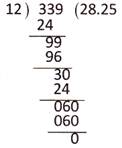
Conversion of a Fraction into Decimals
Divide the numerator by denominator till the remainder becomes zero. If the digits in the numerator goes off, than take other digits as 0 and put the decimal point in the quotient.
Convert \[\frac{339}{12}\] into decimals.
Solution:
You need to login to perform this action.
You will be redirected in
3 sec
