11th Class Mathematics Mathematical Reasoning Notes - Mathematics Olympiads - Matrices and Determinant

 

                                                                                      Matrices and Determinant

 

Key Points to Remember

 

• Matrices & Determinant

 

Let us consider the linear equation

 

\[{{a}_{1}}x+{{b}_{1}}y={{c}_{1}}\]                                    (i)

\[{{a}_{2}}x+{{b}_{2}}y={{c}_{2}}\]                                    (ii)

 

We have one of the methods to solve these equation by cross multiplication method.

 

\[\frac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\frac{y}{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}=\frac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]

 

Now we modify this method & convert this method into standard form (matrix form)

           

• Matrix: Actually it is the shorthend of mathematics. It is an operator as addition, multiplication etc. Every matrix has come into existence through the solution of linear equations.

 

Given linear equation can be solved by matrix method & it is written as,

\[AX=B\]

 

 

• Definition: It is the arrangement of mn things into horizontal (row) vertical (column) wise.

Generally matrix is represented by [ ] (square bracket) or ( ) etc.

 

Generally, it is represented as

\[A=[{{a}_{ij}}]\]          \[i=1,\,2,\,3,....m\]

                                    \[j=1,\,2,\,3,....n\]          

 

Here subscript i denotes no. of row.

& subsrcipt j determines no. of column.

& \[{{a}_{ij}}\to \] represent the position of element a in the given matrix

e.g. \[A=[{{a}_{ij}}]\] & if         \[i\le 3\] and       \[i\le 2\]

 

 

• Order of Matrix: It is the symbol which represent how many rows and columns the matrixs has. In the above example,

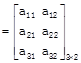
Order of matrix \[A=3\times 2\] in which 3 determine number of row & 2 determine no. of column of given matrix.

 

• Operation of Matrix

 

1. Addition of matrics
2. Subtraction of matrix
3. Multiplication of matrix
4. Adjoint of matrix
5. Inverse of matrixes.

 

• Addition of Matrices

 

Let \[A={{[{{a}_{ij}}]}_{m\times n}}\] & \[B={{[{{b}_{ij}}]}_{m\times n}}\] be two matrices, having same order.

Then \[A+B\] or \[B+A\] is a matrix whose elements be formed through corresponding addition of elements of two given matrices

 

\[A+B=B+A\]

           

 

Similarly for subtraction operation, we can subtracted two matrices.

But \[A-B\ne B-A\] i.e. \[A-B=-(B-A)\]

 

Note: For addition or substraction operation of two or more than two matrices. They (given matrix) should be the same order.

 

• Multiplication operation: Let \[A={{[{{a}_{ij}}]}_{m\times \text{K}}}\] is a matrix of mx k order & \[B={{[{{a}_{ij}}]}_{\text{K}\times \text{P}}}\] is a matrix of \[\text{k}\times p\] order.

For multiplication of two matrices, no. of column of 1st matrix should be equal to no. of row of 2nd matrix. Otherwise multiplication of two matrix does not hold.

Then

 

\[A\times B-[{{c}_{ij}}]\]be a matrix whose order will be\[m\times p\].

 

e.g.       \[A={{\left[ \xrightarrow[2\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,1]{2\,\,\,\,\,\,\,\,\,1\,\,\,\,\,\,\,\,3} \right]}_{2\times 3}}\]

 

 

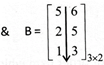
\[\therefore \,\,\,A\times B\]

 

 

 

 

 

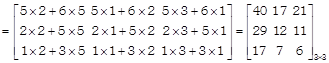
Hence \[A\times B\,\,\ne \,\,B\times A.\]

 

• Type of Matrix

 

(a)        Row Matrix: A matrix having order \[1\times n\] i.e.

Which has only one row, is said to be row matrix.

 

e.g.       \[A={{\left[ 1\,\,\,2\,\,\,3\,\,\,4\,\,\,5 \right]}_{1\times 5}}\]

 

(b)        Column Matrix: A matrix, having and

(m x 1) i.e. which has only one column is said to be column matrix.

 

 

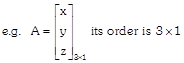
(c)        Square Matrix: A matrix having same no. of row & column is said to be square matrix.

 

 

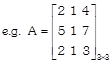
(d)        Diagonal Matrix: A square matrix is said to be diagonal matrix if its non-diagonal elements should be zero.

  

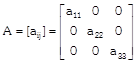
i.e.       \[{{a}_{ij}}=0\] if \[i\ne j\]

 

= something if \[i=j\]

 

• Transpose of a matrix

Let A is a matrix of order\[m\times n\]. Then the transpose of a matrix A is a matrix of order \[n\times m\] which is obtained by interchanging the rows & columns of matrix A. It is denoted by \[A'\] or \[{{A}^{Tau }}\]

 

 

 

• Properties of Transpose of a matrix

 

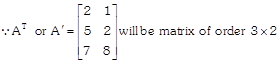
(i)         If A and B be the two matrix of the same order then \[{{(A\pm B)}^{Tau }}={{A}^{Tau }}\pm {{B}^{Tau }}\,\,\,m\times n\]

(ii)        If A be the matrix and k be any scalar quantity then \[{{(\text{k}A)}^{Tau }}=\text{k}\text{.}{{\text{A}}^{Tau }}\]

(iii)       If A & B be two matrix of order \[m\times n\] and \[n\times p\] respectively, there exists the multiplication between A & B. Then

            \[{{(A\times B)}^{Tau }}={{B}^{Tau }}.{{A}^{Tau }}\]

(iv)       The double transpose of any matrix gives its primal matrix i.e. \[{{({{A}^{Tau }})}^{Tau }}=A.\]

 

• Symmetric Matrix: A square matrix A is said to be symmetric if the matrix A is equal to its transpose matrix

i.e. \[A=A'\]

It is represented by

The matrix, \[A={{[{{a}_{ij}}]}_{m\times n}}\] is said to symmetric matrix if \[{{a}_{ij}}={{a}_{j}}.\]

 

 

 

• Skew Symmetric Matrix: A square matrix A is said to be the skew symmetric if the matrix A is equal to its transpose matrix with negative sign.

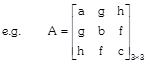
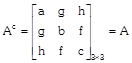
i.e.       \[A=-A'\]

Symbolically, it is represented by

The matrix, \[A={{[{{a}_{ij}}]}_{m\times m}}\] is square matrix.

If \[{{a}_{ij}}=-{{a}_{ij}}\,\,\,\forall \,\,i\And \,j\]

 

e.g.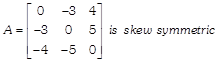     

 

 

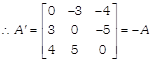
Note:    Every square matrix is written as the sum of the symmetric & skew symmetric matrices.

i.e. If A is a square matrix

 

then \[A=\frac{1}{2}[(A+{{A}^{Tau }})+(A-{{A}^{Tau }})]\]

Where \[A+{{A}^{Tau }}=\] symmetric matrix

& \[A-{{A}^{Tau }}=\] skew symmetric matrix.

Properties of symmetric & skew symmetric matrix.

 

(i)         lf A & B be two symmetric (skew symmetric) matrices A+B be symmetric matrix (skew symmetric matrix).

(ii)        If A is symmetric (or skew symmetric) matrix and k is any scalar quantity, then (kA) is a symmetric (or skew symmetric) matrix.

(iii)       If A and B are symmetric matrices of the same order, the product AB is symmetric iff AB = BA

(iv)       The matrix B' AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.

(v)        If A and Bare symmetric metrices of the same order, then

(a)        AB - BA is a skew symmetric matrix.

(b)        AB + BA is a symmetric matrix.

(vi)       All positive integral powers of a symmetric (skew symmetric) matrix will be symmetric (skew symmetric) matrix.

 

• Singular Matrix: A square matrix is said to be singular matrix if the determinant of A i.e. \[\left| \,A\, \right|\] is zero. i.e. \[\left| \,A\, \right|=0.\]Otherwise, it is a non-singular matrix.

e.g.

 

• Adjoint of a square matrix

 

Let \[A=[{{a}_{ij}}]\] be a square matrix of order m. Then B be a square matrix of order m whose element be the corresponding co-factor element of matrix A. Then the transpose of B is said to be the adjoint at the matrix A.

 

 

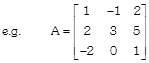
In \[{{R}_{1}}\] row,

co-factor of 1 i.e. \[{{a}_{11}}=3\]

co-factor of -1 i.e. \[{{a}_{12}}=-12\]

co-factor of 2 i.e. \[{{a}_{13}}=6\]

 

In \[{{R}_{2}}\] row,

co-factor of 2 i.e. \[{{a}_{21}}=-\,\,(-1)=2\]

co-factor of 3 i.e. \[{{a}_{22}}=5\]

co-factor of 5 i.e. \[{{a}_{23}}=-\,(-2)=2\]

 

In \[{{R}_{3}}\] row,

co-factor of - 2 i.e. \[{{a}_{31}}=-11\]

co-factor of 0 i.e. \[{{a}_{32}}=-(5-4)=-1\]

co-factor of 1 i.e. \[{{a}_{33}}=3+2=5\]

 

 

 

• Properties of adjoint of a matrix

 

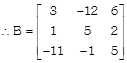
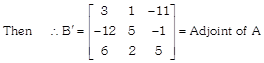
(i)         If A is the square matrix of order m, then adjoint \[A'=(\text{adj}\,\,o\text{f}\,A)\]

(ii)        If A & B be two the square matrices of the same order, then \[\text{adj}(AB)=(\text{adj}\,A).(\text{adj}\,B)\]

(iii)       The adjoint if a diagonal matrix is a diagonal matrix.

(iv)       \[\text{adj}\,\,(\text{adj}\,A)={{\left| \,A\, \right|}^{n-2}}.\] A where A is the non- singular matrix

 

• Inverse of the square a matrix: Let A is the square matrix of order \[m\times m,\]then the square matrix B of order \[m\times m\] is said to be the inverse of the matrix A such that

\[AB=BA=\text{I}\]

Where I is the unit matrix.

i.e. It is represent by \[{{A}^{-1}}\]

 

So,       \[{{A}^{-1}}=\frac{\text{adj}\,o\text{f}\,A}{\left| \,A\, \right|}\]

 

i.e.       \[A.{{A}^{-1}}={{A}^{-1}}.A=\text{I}\]

 

• Properties of inverse matrix

 

(i)         The inverse of the square a matrix exists iff A is non-singular.

 

(ii)        Double inverse of the square matrix is primal matrix A itself.

i.e.       \[{{\left( {{A}^{-1}} \right)}^{-1}}=A\]

 

(iii)       If A & B be two invertiable matrices of the same order m x m then even AB is invertiable in the following order.

\[{{(AB)}^{-1}}={{B}^{-1}}{{A}^{-1}}\]

 

(iv)       The inverse of the transpose of a matrix A is equal to the transpose of the inverse of matrix A.

i.e.       \[{{(A')}^{-1}}=({{A}^{-1}})'\]

 

(v)        If A is the symmetric matrix such that

\[\left| A \right|\ne 0\] then \[{{A}^{-1}}\] is the symmetric matrix.