10th Class Mathematics Triangles

TRIANGLES

FUNDAMENTALS            

Similar figures:

• Figures having the same shape (not necessarily the same size) are called similar figures. Same shapes ensure that the corresponding angles are equal and their corresponding sides are proportional.

Congruent figures:

• Figures having the same shape and the same size are called congruent figures. Here, apart from angles, corresponding sides are also equal

Similar Triangles:

• Two triangles are said to be similar, if their corresponding angles are equal and corresponding sides are proportional.

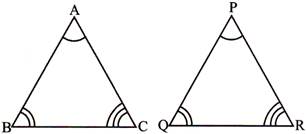
e.g., If in \[\Delta \,ABC\]and \[\Delta \,PQR\]

\[\angle A=\angle P,\angle B=\angle Q,\angle C=\angle R\]

and       \[\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR},\]       then, \[\Delta \text{ }ABC\sim \Delta \,PQR;\] where symbol \[\sim \] is read as ‘is similar to’.

• When two triangles (\[\Delta \text{ }ABC\]and \[\Delta \text{ }DEF\]as below) are similar, then all above results about angles and ratio of sides hold good. However, in questions, when you are asked to prove similarly, you can either prove:

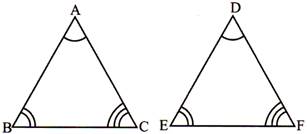
(i) \[\angle A=\angle D,\angle B=\angle E\] (called AA similarly)

Or

(ii) \[\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\] (called SSS similarity)

Or

(iii) \[\frac{AB}{PQ}=\frac{BC}{QR}\] and \[\angle B=\angle Q\] (called SAS similarity)

Any one of the above three, would be sufficient for proving similarity.

Conversely: If \[\Delta \text{ }ABC\]is similar to\[\Delta \text{ }PQR\], then

            \[\angle A=\angle D;\angle B=\angle E;\angle C=\angle Q\] and \[\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\]

• When two triangles are congruent (notation for congruent is \[\cong \])

Then, \[\angle A=\angle D;\text{ }\angle B=\angle E;\text{ }\angle C=\angle F\]

and, \[AB=DE,BC=EF\] and \[CA=FD\]

However, to prove congruency, we need to prove any one of the following only:

(i) \[\text{ }AB=DE,\text{ }BC=EF\And CA=FD\](SSS congruency)

or

(ii) \[AB=DE;\text{ }BC=EF\And \angle B=\angle E\] (SAS congruency)

or

(iii) \[\angle A=\angle D;\angle B=\angle E\] and \[AB=DE\](ASA congruency)

How to look for similarity and congruency of angles

While looking for similarity and congruency, you should not only see external appearance but also which of the corresponding angles are equal (or, which of corresponding sides are in the same ratio).

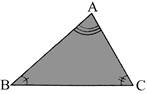
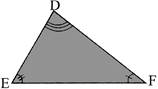
In the above figure, \[\angle B=\angle F;\text{ }\angle C=\angle E\]and \[\angle A\cong \angle D;\] thus \[\Delta \,ACB\cong \Delta \,DEF\](and not\[\Delta \,ABC\cong \Delta \,DEF\])

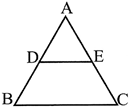
Mathematical statement of the theorem\[\frac{AD}{DB}=\frac{AE}{EC}\] (where\[DE\parallel ~BC\])

i.e., if in \[\Delta \text{ }ABC\]as shown above, \[DE\parallel BC\Rightarrow \frac{AD}{DB}=\frac{AE}{EC}\]

Converse of Basic Proportionality Theorem:

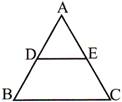
Mathematical statement of the theorem if in \[\Delta \,ABC\](as shown above),

\[\frac{AD}{DB}=\frac{AE}{EC}\Rightarrow DE\parallel BC)\]