10th Class Mathematics Pair of Linear Equations in Two Variables Linear Equation in two Variables

 LINEAR EQUATION IN TWO VARIABLES

FUNDAMENTALS

While solving the problems, in most cases, first we need to frame an equation. Therefore, we will learn how to frame and solve equations sometimes. Framing an equation is more crucial aspect after which solving the equation may be quite easy.

Algebraic Expression

Expression of the form, \[3x,(3x+6),(2x-6y),3{{x}^{2}}+3\sqrt[3]{y},\frac{7{{x}^{6}}}{3}\sqrt{y}\] are algebraic expressions. \[3x\] and 6 are the terms of \[\left( 3x+6 \right)\] and 2x and 6y are the terms of\[2x-6y\]. Algebraic expressions are made of numbers, symbols and the basic arithmetical operations. In the term 3x, 3 is the numerical coefficient of x and x is the variable coefficient of 3.

The following step are involved in solving an equation.

Step – 1: Always ensure that the unknown quantities are on the LHS and the known quantities or constants on the RHS.

Step – 2: Add all the terms containing the unknowns on the LHS and all the known on the RHS. So that each side of the equation contains only one term.

Step – 3: Divide both sides of the equation by the coefficient of the unknown.

Example: lf\[4x+15=35\], then find the value of x

Solution:          Step – 1: Group the known quantities as the RHS of the equation, i.e.,\[~4x=35-15\]

Step – 2: Simplify the numbers on the RHS\[\Rightarrow 4x=20\].

Step – 3: Since 4 is the coefficient of x, divide both the sides of the equation by 4.

Linear equation in two variables

An equation of the form\[ax+by=c\], where \[a\ne 0,b\ne 0\]and a, b and c are real numbers is known as a linear equation in two variables x and y.

A pair of linear equations in two variables

Two linear equations in the same two variables (x, y) are called a pair of linear equations.

General form of a pair of linear equations in two variables

The general form of a pair of linear equations in two variables is \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\], where \[{{a}_{1}},{{a}_{2}},{{b}_{1}},{{b}_{2}},{{c}_{1}}\] and \[{{c}_{2}}\] are real numbers such that \[a_{1}^{2}+b_{1}^{2}\ne 0\] and \[a_{2}^{2}+b_{2}^{2}\ne 0\].

Methods of solving a pair of linear equations in two variables: A pair of linear equations in two variables can be solved by (i) Graphical method (ii) Algebraic method.

(i) Graphical method: The graph of a linear equation is a straight line. The graph of a pair of linear equations in two variables is represented by two lines.

(a) If the two lines coincide, then the pair of linear equations has infinitely many solutions (each point on the line being a solution), and is said to be dependent or consistent.

(b) If the lines are parallel, then the pair of linear equations has no solution (no common point) and is said to be inconsistent.

In other words, there are three types of solutions of a pair of linear equations in two variables

(a) Unique solution          (b) Infinitely many solutions         (c) No solutions

(ii) Algebraic methods: To obtain the exact solution of simultaneous linear equations, algebraic methods are used.

There are three algebraic methods:

(a) Elimination by substitution method.

(b) Elimination by equating the coefficients method.

(c) Cross multiplication method.

Cross - Multiplication Method:

Solve \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\], where \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}.\]

Solution: Given, \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\]     and,    \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]

Solving the above equations using Elimination by substitution method, we get,

\[x=\frac{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\] and \[y=\frac{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]; which can be written as,

\[\frac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\frac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\] and \[\frac{y}{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}=\frac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]

\[\Rightarrow \frac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\frac{y}{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}=\frac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]

            The above result can be better remembered using the Fig.

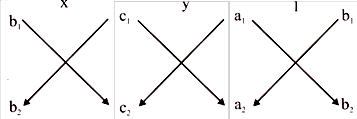
The arrow between the two numbers indicates that they are to be multiplied and second produced is  to be subtracted from the first. Thus, for memory, steps are as below:

Step – 1: Write the given equations in the form \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\].

Step – 2: Write the coefficients \[({{a}_{1}},{{b}_{1}},{{c}_{1}})\] and \[({{a}_{2}},{{b}_{2}},{{c}_{2}})\] as mentioned above.

Step – 3: Find the values of x and y.

Conditions on possibility of solving of a pair of linear equations in two variables

Consider the pair of linear equation.

            \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0;{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]