10th Class Mathematics Coordinate Geometry

 

Coordinate Geometry

 

Coordinate Geometry

 

1. Abscissa: The distance of a point from the y-axis is called the x-coordinate or abscissa of that point.

 

2. Ordinate: The distance of a point from the x-axis is called the y-coordinate or ordinate of that point.

 

3. Collinear Points: Three or more points are said to be collinear if they lie on the same straight line.

 

4. Centroid of a triangle: The point of intersection of all the medians of a triangle is called its centroid.

 

5. Distance Formula: The distance between two points \[P({{x}_{1}}\,,\,\,{{y}_{1}})\,\,and\,\,Q({{x}_{2}},\,\,{{y}_{2}})\] is given by

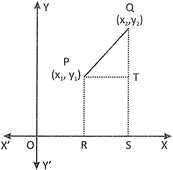
            \[PQ\,=\,\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}\,+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]  

           

           

 

6. Test for Collinearity of Three Points: To show that any three given points P, Q and R are collinear, we find the        distance PQ, QR and PR and show that any one of these distance is equal to the sum of the other two.

 

7. Section Formula: The coordinates of the point \[P\left( x,\text{ }y \right)\] which divides the line segment joining the points \[A({{x}_{1}}^{,}\,{{y}_{1}})\,\,and\,\,B({{x}_{2}},\,{{y}_{2}})\], internally, in the ratio \[{{m}_{1}}:\text{ }{{m}_{2}}\] are given by

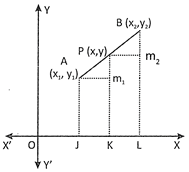
\[\frac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}},\,\frac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}}\]

                                                           

 

8. Midpoint Formula: The midpoint of a line segment joining the points \[P\left( {{x}_{1}},\text{ }{{y}_{1}} \right)\] and \[Q({{x}_{2}},\,{{y}_{2\,\,}})\,is\,\,\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\,\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]       

 

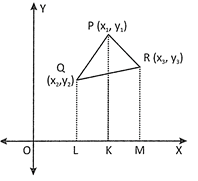
9.         Area of a Triangle: The area of a \[\Delta \,PQR\] having vertices points \[P({{x}_{1}},\,\,{{y}_{1}}),\,Q({{x}_{2}},\,\,{{y}_{2}})\] and \[R({{x}_{3}},\,\,{{y}_{3}})\] is the numerical value of the expression \[\left| \frac{1}{2}\{{{x}_{1}}({{y}_{2}}-{{y}_{3}})+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}})\} \right|\]

             

 

Snap Test

 

 

1. Find the coordinates of the point which divides the line segment joining the points \[\left( \mathbf{6},\text{ }\mathbf{3} \right)\text{ }\mathbf{and}\text{ }\left( -\mathbf{4},\text{ }\mathbf{5} \right)\] in the ratio \[\mathbf{3}\text{ }:\text{ }\mathbf{2}\] internally.

 

            (a) \[\left( 0,\,\,\frac{21}{5} \right)\]                     

(b) \[\left( 1,\,\,\frac{21}{5} \right)\]

            (c) \[\left( 1,\,\,\frac{21}{4} \right)\]                     

(d) \[\left( 2,\,\,\frac{21}{4} \right)\]

            (e) None of these

Ans.     (a)

Explanation: Let AB be the line segment with end points \[A\left( 6,\text{ }3 \right)\text{ }and\text{ }B\text{ }\left( -\text{ }4,\text{ }5 \right).\]

Then, \[\left( {{x}_{1}}=\text{ }6,\text{ }{{y}_{1}}=\text{ }3 \right)\] and \[\left( {{x}_{2}}=-\text{ }4,\text{ }{{y}_{2}}=\text{ }5 \right)\].

            Also, \[{{m}_{1}}=\text{ }3\text{ }and\text{ }{{m}_{2}}=\text{ }2\].

            Let the required point be \[P\text{ }\left( x,\text{ }y \right)\].

            By section formula:

\[x=\frac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}},\,\,y\,\,=\frac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}}\]

\[x\,\,=\,\,\frac{3\times (-4)+2\times 6}{(3+2)},\,\,y\,\frac{(3\times 5+2\times 3)}{(3+2)}\,\,\,\Rightarrow \,x=0,\,\,y=\frac{21}{5}\]

            Hence, the required point is \[P\left( 0,\,\,\frac{21}{5} \right)\]

 

2. Find the ratio in which the point \[\left( -\mathbf{3},\text{ }\mathbf{k} \right)\] divides the line segment joining the points \[\left( -\mathbf{5},\text{ }-\mathbf{4} \right)\]     and \[\left( -\mathbf{2},\text{ }\mathbf{3} \right)\].

            (a) \[3\text{ }:\text{ }1\]            

(b) \[1\text{ }:\text{ }1\]

            (c) \[2\text{ }:\text{ }1\]             

(d) \[2\text{ }:\text{ }2\]

            (e) None of these

Ans.     (b)

Explanation: Let P \[\left( -\text{ }3,\text{ }k \right)\] divide the line segment \[A\left( -\text{ }5,\text{ }-4 \right)\] and \[B\text{ }\left( -\text{ }2,\text{ }3 \right)\] in the ratio \[m\text{ }:\text{ }1\],

 

            Then the coordinates of P are given by \[\left( \frac{-2m-5}{m+1},\,\,\frac{3m-4}{m+1} \right)\].

            But, we are given \[P\left( -\text{ }3,\text{ }k \right)\].

 

            \[\therefore \,\,\,\,\,\frac{-2m-5}{m+1}=\,\,-3\,\,and\,\,\,\frac{3m-4}{m+1}\,\,=\,\,k\]

 

Now, \[\frac{-2m-5}{m+1}=-\text{ }3\text{ }\Rightarrow \,\,-2m\text{ }-\text{ }5\text{ }=-\text{ }3m\text{ }-\text{ }1\text{ }\Rightarrow \text{ }2m\text{ }=\text{ }4\text{ }\Rightarrow \text{ }m=2.\]

 

            So, the required ratio is \[2\text{ }:\text{ }1\].

 

 

 

3. Which one of the following groups of points are collinear?

            (a) \[\left( 1,\text{ }-1 \right),\text{ }\left( 5,\text{ }2 \right)\text{ }and\text{ }\left( 3,\text{ }5 \right)\]

(b) \[\left( 1,\,-1 \right),\text{ }\left( 5,\text{ }2 \right)\text{ }and\text{ }\left( 5,\text{ }5 \right)\]

            (c) \[\left( 1,\text{ }-1 \right),\text{ }\left( 5,\text{ }2 \right)\text{ }and\text{ }\left( 9,\text{ }5 \right)\] 

(d) \[\left( 1,-\text{ }1 \right),\left( 5,\text{ }2 \right)\text{ }and\text{ }\left( 6,\text{ }5 \right)\]           

            (e) None of these

Ans.     (c)

Explanation: Let \[P\left( 1,\text{ }-\text{ }1 \right),\text{ }Q\left( 5,\text{ }2 \right)\text{ }and\text{ }R\left( 9,\text{ }5 \right)\] be the given points. Then,

\[PQ=\sqrt{{{(5-1)}^{2}}+{{[2-(-1)]}^{2}}}\,\,=\sqrt{{{4}^{2}}+{{3}^{2}}}\,\,=\,\,\sqrt{25}=5\,units,\]

\[QR=\sqrt{{{(9-5)}^{2}}+(5-2){{]}^{2}}}\,\,=\,\,\sqrt{{{4}^{2}}+{{3}^{2}}}\,\,=\,\,\sqrt{25}=5\,units,\]

\[PR\,\,\,\,=\,\,\,\,\sqrt{{{(9-1)}^{2}}+{{[5-(-1)]}^{2}}}\,\,=\,\,\,\sqrt{{{8}^{2}}+{{6}^{2}}}\,\,=\,\,\,\sqrt{100}\,\,\,=\,\,10\,\,units\]

\[\therefore \,\,\,\,\,PQ+QR\text{ }=\left( 5\text{ }+\text{ }5 \right)\text{ }units\text{ }=10\text{ }units\text{ }=\text{ }PR\]              

            Hence, the given points A, B, C are collinear.

 

4. If \[\left( -\mathbf{2},\text{ }-\mathbf{1} \right),\text{ }\left( \mathbf{a},\text{ }\mathbf{0} \right),\text{ }\left( \mathbf{4},\text{ }\mathbf{b} \right)\text{ }\mathbf{and}\text{ }\left( \mathbf{1},\text{ }\mathbf{2} \right)\] are the vertices of a parallelogram, find the value of a and b.

(a) \[a\text{ }=\text{ }1,\text{ }b\text{ }=\text{ }3\]       

(b) \[a\text{ }=\text{ }1,\text{ }b\text{ }=\text{ }5\]

            (c) \[a\text{ }=\text{ }3,\text{ }b\text{ }=\text{ }1\]       

(d) \[a\text{ }=\text{ }2,\text{ }b\text{ }=\text{ }4\]

            (e) None of these

Ans.     (a)

Explanation: In the following figure. Let \[P\left( -2,\text{ }-1 \right),\text{ }Q\text{ }\left( a,\text{ }0 \right),\text{ }R\left( 4,\text{ }b \right)\text{ }and\text{ }S\left( 1,\text{ }2 \right)\] be the vertices of a parallelogram PQRS.

            Join the diagonals PR and QS, intersecting each other at the point O.

 

           

           

          

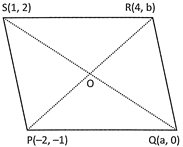
We know that the diagonals of a parallelogram bisect each other.

            Therefore, 0 is the mid-point of AC as well as that of BD.

Now, mid-point of PR is \[\left( \frac{-2+4}{2},\,\,\frac{-1+b}{2} \right)\,i.e.\,\left( 1,\,\,\frac{b-1}{2} \right)\]

And, mid-point of QS is \[\left( \frac{a+1}{2},\,\,\frac{0+2}{2} \right)\,i.e.\,\left( \frac{a+1}{2}\,\,,\,\,1\, \right)\].

            \[\therefore \,\,\,\,\frac{a+1}{2}=1\,\,\,and\,\,\,\frac{b-1}{2}\,\,\,=\,\,\Rightarrow \,\,a=1\,\,and\,\,b=3.\]

           

5. The vertices of a triangle are \[\left( -\mathbf{1},\text{ }\mathbf{3} \right),\text{ }\left( \mathbf{1},\text{ }-\mathbf{1} \right)\text{ }\mathbf{and}\text{ }\left( \mathbf{5},\text{ }\mathbf{1} \right)\]. Find the lengths of medians through the vertices \[\left( -\mathbf{1},\text{ }\mathbf{3} \right)\text{ }\mathbf{and}\text{ }\left( \mathbf{5},\text{ }\mathbf{1} \right)\].

            (a) 3 units, 3 units           (b) 6 units, 6 units

            (c) 5 units, 5 units           (d) 4 units, 4 units

            (e) None of these

Ans.     (c)

Explanation: in the following figure, Let \[A\left( -1,\text{ }3 \right),\text{ }B\left( 1,\text{ }-1 \right)\text{ }and\text{ }C\left( 5,\text{ }1 \right)\] be the three vertices of a \[\Delta \,ABC\] Let D and E be the mid-points of the sides BC and AB respectively.

 

           

 

           

The coordinates of \[D\,\,=\,\,\left( \frac{1+5}{2},\,\,\frac{-1+1}{2} \right)\]

i.e. \[\left( 3,\text{ }0 \right)\] and those of E are \[\left( \frac{-1+1}{2},\,\,\frac{3-1}{2} \right)\] i.e. \[\left( 0,\text{ }1 \right)\].

            \[\therefore \] Length of median through \[A\left( -1,\text{ }3 \right)\]

\[=\,\,\,AD\,\,\,=\sqrt{{{[3-(-1)]}^{2}}+{{(0-3)}^{2}}}=\sqrt{{{4}^{2}}+{{(-3)}^{2}}}\,\,=\,\,\,\sqrt{16+9}\,\,\,=\,\,\,\sqrt{25}\,\,=\,\,5\,\,units.\]

            Length of median through \[C\text{ }\left( 5,\text{ }1 \right)\]

\[=\,\,CE\,\,=\,\,\,\sqrt{{{(0-5)}^{2}}+{{(1+1)}^{2}}}\,\,\,=\,\,\,\sqrt{{{(-5)}^{2}}+0}\,\,\,\,=\,\,\sqrt{25}\,\,\,=\,\,5\,\,units\].