10th Class Mathematics Areas Related to Circles Area of Circle

AREA OF CIRCLE

FUNDAMENTALS

Perimeter and Area of a Circle

The distance covered by travelling once around a circle is called its perimeter, and in case of a circle, it is usually called its circumference. The circumference of a circle bears a constant ratio with its diameter. This constant ratio is denoted by the Greek letter \[\pi \] (read as ‘pi’), m other words,

\[\frac{circumference}{diameter}=\pi \]

Or         \[circumference=\pi \times diameter\]

\[=\pi \times 2r\] (where r is the radius of the circle) \[=2\pi r\]

The great Indian mathematician Aryabhatta (A. D. 476 – 550) gave an approximate value of \[\pi \] He stated that \[\pi =\frac{62832}{20000}\], which is nearly equal to 3.1416. It is also interesting to note that using an identity of the great mathematical genius Srinivas Ramanujan (1887 – 1920) of India, mathematicians have been able to calculate the value of n correct to million places of decimals. As you known from Chapter I of Class IX, n is an irrational number and its decimal expansion is non – terminating and non – recurring (non – repeating). However, for practical purposes, we generally take the value of \[\pi \] as \[\frac{22}{7}\] or 3.14, approximately.

Areas of Sector and Segment of a Circle

The portion (or part) of the circular region enclosed by two radii and the corresponding arc is called sector of the circle and the portion (or part) of the circular regions enclosed between a chord and the corresponding arc is called a segment of the circle.

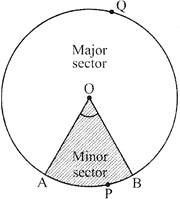
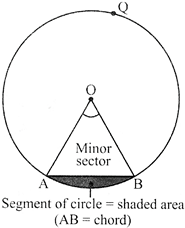
Thus, in figure shaded region OAPB is a sector of the circle with centre O. \[\angle AOB\]is called the angle of the sector. Note that in this figure, unshaded region OAQB is also a sector of the circle. For obvious reasons, OAPB is called the minor sector and OAQB is called the major sector. You can also see that angle of the major sector is (\[360{}^\circ -\angle AOB\]).

Now, look at figure in which AB is a chord of the circle with centre O. So, shaded region APB is a segment of the circle. You can also note that unshaded region AQB is another segment of the circle formed by the chord AB. For obvious reasons, APB is called the minor segment and AQB is called the major segment.

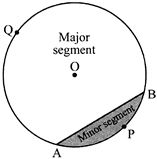
Remarks: When we write ‘segment’ and ‘sector’ we will mean the ‘minor segment’ and the ‘minor sector’ respectively, unless stated otherwise.

Calculating area of sector of a circle

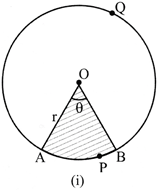
Let OAPB be a sector of a circle with centre O and radius r (see figure). Let the degree measure of \[\angle AOB\] be \[\theta \].

You know that area of a circle (in fact of a circular regions or disc) is \[\pi {{r}^{2}}\].

In a way, we can consider this circular region to be a sector forming an angle of \[360{}^\circ \] (i.e., of degree measure 360) at the centre O. Now by applying the Unitary Method, we can arrive at the area of the sector OAPB as follows:

When degree measure of the angle at the centre is\[360{}^\circ \], area of the sector \[={{r}^{2}}\]

So, when the degree measure of the angle at the centre is \[1{}^\circ \], area of the sector \[=\frac{\pi {{r}^{2}}}{360}\].

Therefore, when the degree measure of the angle at the centre is \[\theta \], area of the sector \[=\frac{\pi {{r}^{2}}}{360}\times \theta =\frac{\theta }{360}\times \pi {{r}^{2}}\]

Thus, we obtain the following relation (or formula) for area of a sector of a circle:

Area of the sector of angle \[\theta =\frac{\theta }{360}\times \pi {{r}^{2}}\],

Calculating length of arc of a circle

Let ‘r’ be the radius of the circle and \[\theta \] the angle of the sector in degrees.

Now, a natural equation arises: Can we find the length of the arc APB corresponding to this sector OAPB? The answer is yes. Again, by applying the Unitary Method and taking the whole length of the circle (of angle \[360{}^\circ \]) as \[2\pi r\], we can obtain the required length of the arc APB as \[\frac{\theta }{360}\times 2\pi r\].

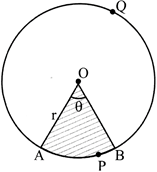(ii)                 (ii)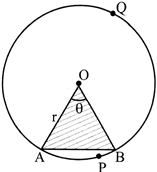

 Length of an arc of a sector of angle \[\theta =\frac{\theta }{360}\times 2\pi r\]

Calculating area of segment of a circle

Now let us take the case of the area of the segment APB of a circle with centre O and radius r (see above figure). You can see that:

Area of the segment APB = Area of the sector OAPB – Area of \[\Delta \,OAB\]

                                    \[=\frac{\theta }{360}\times \pi {{r}^{2}}-\text{area}\,\,\text{of}\,\,\Delta \,OAB\]

Note: From figure (ii) to (iii) respectively, you can observe that:

Area of the major sector \[OAQB=\pi {{r}^{2}}\] – Area of minor sector OAPB

And, Area of major segment \[AQB=\pi {{r}^{2}}\]– Area of the minor segment APB

Areas of Combinations of Plane Figure

So far, we have calculated the areas of different figures separately. Let us now try to calculate the areas of some combinations of plane figures. We come across these types of figures in our daily life and also in the form of various interesting designs. Flower beds, drain covers, window design, design on table covers, are some of such examples. We illustrate the process of calculating areas of these figures through some examples.

A quick look at relevant formula:

Circle and semi - Circle

Area of circle \[=\pi {{r}^{2}}sq.\]units.

2. Area of the semi-circle \[=\frac{\pi {{r}^{2}}}{2}sq.\] units.
3. Circumference of the circle \[=2\pi r\] units \[=\pi d\]units.
4. Circumference of the semicircle \[=\left( \pi +2 \right)r\] units\[=\frac{36r}{7}\text{units}\]

(Where r is radius and d is diameter)

Circular Ring    

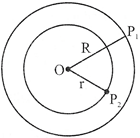
Area of the ring \[=\pi \left( {{R}^{2}}-{{r}^{2}} \right)=\pi \left( R+r \right)\left( R-r \right)\]

(Where R and r are outer and inner radii of a ring and (R – r) is the width of the ring)

Sector and Segments

1. Arc length \[\overset\frown{ACB}\]

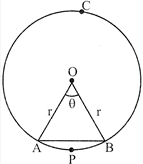
      \[1=\left( \frac{\theta }{360{}^\circ } \right)2\pi r\] units

2. Area of the sector OAPB

      \[A=\left( \frac{\theta }{360{}^\circ } \right)\pi {{r}^{1}}sq.\] units.

3. Perimeter of the sector \[=[\left( 1+2r \right)\] units.
4. Area of the segment APB = (A – Area of the \[\Delta \,AOB\]) sq. units.
5. Perimeter of the segment ACB = (Arc length ACB + AB) units.

Rotations Made by a Wheel

1. Distance covered by a wheel in one revolution = Circumference of the wheel.
2. Number of rotations made by a wheel in unit time \[\text{=}\frac{\text{Distance}\,\,\text{covered}\,\,\text{by}\,\,\text{it}\,\,\text{in}\,\,\text{unit}\,\,\text{time}}{\text{Circumference}\,\,\text{of}\,\,\text{the}\,\,\text{wheel}}\]
3. Angle made by minute hand in one minute \[\text{=}\frac{360{}^\circ }{60}=6{}^\circ \].
4. Angle made by hour hand in one minute \[\text{=}\frac{30{}^\circ }{60}={{\left( \frac{1}{2} \right)}^{0}}\].

Equilateral\[\Delta \]

1. Radius of in-circle (GE) of equilateral triangle \[=\frac{1}{3}\left( \frac{\sqrt{3}a}{2} \right)=\frac{a}{2\sqrt{3}}\] units.
2. Circum - radius (AG) of equilateral triangle \[=\frac{2}{3}\left( \frac{\sqrt{3}a}{2} \right)=\frac{a}{\sqrt{3}}\] units. (Where a is side of the triangle).