question_answer

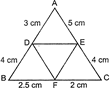
In the given figure, \[AD=3cm,\,\,AE=5cm,\,\,BD=4cm,\,\,CE=4cm,\,\,CF=2cm,\,\,BF=2.5cm\], then find the pair of parallel lines and hence their lengths.

Answer:

\[\frac{EC}{EA}=\frac{CF}{FB}\]  and \[\frac{CF}{FB}=\frac{2}{2.5}=\frac{4}{5}\]

\[\Rightarrow \frac{EC}{EA}=\frac{CF}{FB}\]

In \[\Delta \text{ }ABC,\text{ }EF\parallel AB\]

[Converse of Thales' theorem]

Also,     \[\frac{CE}{CA}=\frac{4}{4+5}=\frac{4}{9}\]

\[\frac{CE}{CB}=\frac{2}{2+2.5}=\frac{2}{4.5}=\frac{4}{9}\]

\[\frac{EC}{EA}=\frac{CF}{CB}\]

\[\angle ECF=\angle ACB\]                                  [Common]

\[\Delta \text{ }CFE\tilde{\ }\Delta \text{ }CBA\]                   [SAS similarity]

\[\Rightarrow \frac{EF}{AB}=\frac{CE}{CA}\]

[In similar \[\Delta 's\], corresponding sides are proportional]

\[\Rightarrow \frac{EF}{7}=\frac{4}{9}\]

\[[\because ~\,AB=3+4=7\text{ }cm]\]

\[\therefore EF=\frac{28}{9}cm\] and \[AB=7\,cm\]