Answer:
\[A{{C}^{2}}=B{{C}^{2}}-A{{B}^{2}}\] [Given] \[A{{C}^{2}}+A{{B}^{2}}=B{{C}^{2}}\] \[\therefore \angle BAC=90{}^\circ \] [By converse of Pythagoras? theorem] \[\Delta \,APB\sim \Delta \,CPA\] 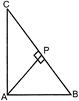
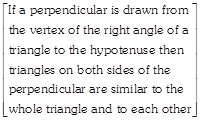
\[\Rightarrow \frac{AP}{CP}=\frac{PB}{PA}\] [In similar triangle, corresponding sides are proportional] \[\Rightarrow P{{A}^{2}}=PB.CP\] Hence Proved.
You need to login to perform this action.
You will be redirected in
3 sec
