question_answer

If an isosceles triangle of vertical angle 29 is inscribed in a circle of radius a. Then, area of the triangle is maximum, when \[\left[ -\frac{1}{2},1 \right]\] is equal to

A) \[\omega \]       

B) \[(1+\omega )(1+{{\omega }^{2}}(1+{{\omega }^{3}})(1+{{\omega }^{4}})\]

C) \[(1+{{\omega }^{5}})...(1+{{\omega }^{3n}})\]                                

D) \[{{2}^{3n}}\]

Correct Answer: A

Solution :

We have, \[AD=a+a\cos 2\theta \]and \[BC=2a\sin 2\theta \] \[\therefore \]Area of \[\Delta ABC\]is given by \[\Delta =\frac{1}{2}BC\times AD=\frac{2}{2}{{a}^{2}}(\sin 2\theta +\sin 2\theta \cos 2\theta )\] \[\Rightarrow \]\[\Delta ={{a}^{2}}\sin 2\theta +\frac{1}{2}{{a}^{2}}\sin 4\theta \]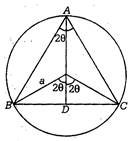 On differentiating both sides w.r.t. \[\theta \], we get \[\frac{d\Delta }{d\theta }=2{{a}^{2}}\cos 2\theta +2{{a}^{2}}\cos 4\theta \] For maximum or minimum, put \[\frac{d\Delta }{d\theta }=0\]. \[\Rightarrow \]\[\cos 2\theta =-\cos 4\theta \]\[\Rightarrow \]\[2\theta =\pi -4\theta \]\[\Rightarrow \]\[\theta =\frac{\pi }{6}\] Now,\[\frac{{{d}^{2}}\Delta }{d{{\theta }^{2}}}=-2{{a}^{2}}\sin 2\theta \times 2-2{{a}^{2}}\sin 4\theta \times 4\] \[=-4{{a}^{2}}\sin 2\theta \times 8-8{{a}^{2}}\sin 4\theta \] At\[\theta =\frac{\pi }{6},\frac{{{d}^{2}}\Delta }{d{{\theta }^{2}}}=-4{{a}^{2}}\sin \frac{\pi }{3}-8{{a}^{2}}\sin \frac{2\pi }{3}\] \[=-4{{a}^{2}}\times \frac{\sqrt{3}}{2}-8{{a}^{2}}\times \frac{\sqrt{3}}{2}\] \[=-6{{a}^{2}}\sqrt{3}<0\] Hence, \[\Delta \] is maximum for \[\theta =\frac{\pi }{6}.\]