A) \[10\sqrt{5}\]
B) \[\frac{100}{3\sqrt{3}}\]
C) \[20\]
D) \[25\]
Correct Answer: C
Solution :
\[\cot \alpha =3\sqrt{2}\]\[\And cosec\beta =2\sqrt{2}\]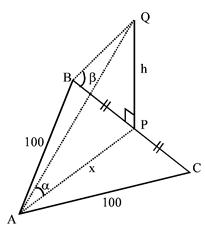 So,\[\frac{x}{h}=3\sqrt{2}\] ...(i) And \[\frac{h}{\sqrt{{{10}^{4}}-{{x}^{2}}}}=\frac{1}{\sqrt{7}}\] ?(ii) So, from (i) & (ii) \[\Rightarrow \frac{h}{\sqrt{{{10}^{4}}-18{{h}^{2}}}}=\frac{1}{\sqrt{7}}\]\[\Rightarrow 25{{h}^{2}}=100\times 100\] \[\Rightarrow h=20.\]
So,\[\frac{x}{h}=3\sqrt{2}\] ...(i) And \[\frac{h}{\sqrt{{{10}^{4}}-{{x}^{2}}}}=\frac{1}{\sqrt{7}}\] ?(ii) So, from (i) & (ii) \[\Rightarrow \frac{h}{\sqrt{{{10}^{4}}-18{{h}^{2}}}}=\frac{1}{\sqrt{7}}\]\[\Rightarrow 25{{h}^{2}}=100\times 100\] \[\Rightarrow h=20.\]
You need to login to perform this action.
You will be redirected in
3 sec
