A) \[\frac{M{{R}^{2}}}{6}\]
B) \[\frac{M{{R}^{2}}}{3}\]
C) \[\frac{2M{{R}^{2}}}{3}\]
D) \[\frac{M{{R}^{2}}}{2}\]
Correct Answer: C
Solution :
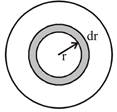 \[{{I}_{Disc}}=\int\limits_{0}^{R}{(dm)}\,{{r}^{2}}\Rightarrow {{I}_{Disc}}=\int\limits_{0}^{R}{(\sigma 2\pi rdr)}{{r}^{2}}\] \[{{I}_{Disc}}=\int\limits_{0}^{R}{(k}{{r}^{2}}2\pi rdr){{r}^{2}}\]Mass of disc \[{{I}_{Disc}}=2\pi k\int\limits_{0}^{R}{{{r}^{5}}}dr\,\,\,\,\,\,\,\,\,\,\,\,\,\,M=\int\limits_{0}^{R}{(}2\pi rdr)k{{r}^{2}}\] \[{{I}_{Disc}}=2\pi k\left( \frac{{{r}^{6}}}{6} \right)_{0}^{R}\,\,\,\,\,\,\,\,\,\,\,\,\,M=2\pi k\int\limits_{0}^{R}{{{r}^{3}}dr}\] \[{{I}_{Disc}}=2\pi k\frac{{{R}^{6}}}{6}\,\,\,\,\,\,\,\,\,\,\,\,\,\left. \,\,\,\,\,\,\,M=2\pi k\frac{{{r}^{4}}}{4} \right|_{0}^{R}\] \[{{I}_{Disc}}=\frac{\pi k{{R}^{6}}}{3}=\left( \frac{\pi k{{R}^{4}}}{2} \right)\frac{{{R}^{2}}2}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M=2\pi k\frac{{{R}^{4}}}{4}\] \[{{I}_{Disc}}=\frac{M2{{R}^{2}}}{3}\] \[{{I}_{Disc}}=\frac{2}{3}M{{R}^{2}}\]
\[{{I}_{Disc}}=\int\limits_{0}^{R}{(dm)}\,{{r}^{2}}\Rightarrow {{I}_{Disc}}=\int\limits_{0}^{R}{(\sigma 2\pi rdr)}{{r}^{2}}\] \[{{I}_{Disc}}=\int\limits_{0}^{R}{(k}{{r}^{2}}2\pi rdr){{r}^{2}}\]Mass of disc \[{{I}_{Disc}}=2\pi k\int\limits_{0}^{R}{{{r}^{5}}}dr\,\,\,\,\,\,\,\,\,\,\,\,\,\,M=\int\limits_{0}^{R}{(}2\pi rdr)k{{r}^{2}}\] \[{{I}_{Disc}}=2\pi k\left( \frac{{{r}^{6}}}{6} \right)_{0}^{R}\,\,\,\,\,\,\,\,\,\,\,\,\,M=2\pi k\int\limits_{0}^{R}{{{r}^{3}}dr}\] \[{{I}_{Disc}}=2\pi k\frac{{{R}^{6}}}{6}\,\,\,\,\,\,\,\,\,\,\,\,\,\left. \,\,\,\,\,\,\,M=2\pi k\frac{{{r}^{4}}}{4} \right|_{0}^{R}\] \[{{I}_{Disc}}=\frac{\pi k{{R}^{6}}}{3}=\left( \frac{\pi k{{R}^{4}}}{2} \right)\frac{{{R}^{2}}2}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M=2\pi k\frac{{{R}^{4}}}{4}\] \[{{I}_{Disc}}=\frac{M2{{R}^{2}}}{3}\] \[{{I}_{Disc}}=\frac{2}{3}M{{R}^{2}}\]
You need to login to perform this action.
You will be redirected in
3 sec
