2. Solved Papers
  3. JEE Main & Advanced

JEE Main & Advanced JEE Main Paper (Held on 10-4-2019 Morning)

  • question_answer
    SOLUTION A bacterial infection in an internal wound grows as \[N'(t)={{N}_{0}}\] exp(t), where the time t is in hours. A dose of antibiotic, taken orally, needs 1 hour to reach the wound. Once it reaches there, the bacterial population goes down as \[\frac{dN}{dt}=-5{{N}^{2}}.\]What will be the plot of \[\frac{{{N}_{0}}}{N}\]vs. t after 1 hour ? [JEE Main 10-4-2019 Morning]

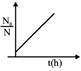
    A)

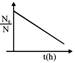
    B)

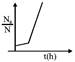
    C)                 

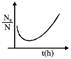
    D)

    Correct Answer: A

    Solution :

    From 0 to 1 hour, \[N'={{N}_{0}}{{e}^{t}}\] From 1 hour onwards\[\frac{dN}{dt}=-5{{N}^{2}}\] So at t = 1 hour, \[N'=e{{N}_{0}}\] \[\frac{dN}{dt}=-5{{N}^{2}}\] \[\int\limits_{e{{N}_{0}}}^{N}{{{N}^{-2}}}dN=-5\int\limits_{1}^{t}{dt}\] \[\frac{1}{N}-\frac{1}{e{{N}_{0}}}=5(t-1)\] \[\frac{{{N}_{0}}}{N}-\frac{1}{e}=5{{N}_{0}}(t-1)\] \[\frac{{{N}_{0}}}{N}=5{{N}_{0}}(t-1)+\frac{1}{e}\] \[\frac{{{N}_{0}}}{N}=5{{N}_{0}}t+\left( \frac{1}{e}-5{{N}_{0}} \right)\]    which is following \[y=mx+C\]             


You need to login to perform this action.
You will be redirected in 3 sec spinner