question_answer

Assuming the sun to be a spherical body of radius R at a temperature of T K, evaluate the total radiant power, incident on earth, at a distance r from the sun.

A) \[4\pi r_{0}^{2}{{R}^{2}}\sigma {{T}^{4}}/{{r}^{2}}\]        

B) \[\pi r_{0}^{2}{{R}^{2}}\sigma {{T}^{4}}/{{r}^{2}}\]

C)        \[r_{0}^{2}{{R}^{2}}\sigma {{T}^{4}}/4\pi {{r}^{2}}\]

D)        \[{{R}^{2}}\sigma {{T}^{4}}/{{r}^{2}}\] where, \[{{r}_{0}}\] is the radius of the earth and a is Stefan's constant.

Correct Answer: B

Solution :

From Stefan's law, the rate at which energy is radiated by the sun at its surface is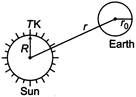 \[P=\sigma \times 4\pi {{R}^{2}}\times {{T}^{4}}\] (sun is a perfectly black body as it emits radiations of all wavelengths and so for it\[e=1\])   The intensity of this power at the earth's surface (under the assumption\[r>>{{r}_{0}}\]is \[I=\frac{P}{4\pi {{r}^{2}}}=\frac{\sigma \times 4\pi {{R}^{2}}{{T}^{4}}}{4\pi {{r}^{2}}}=\frac{\sigma {{R}^{2}}{{T}^{4}}}{{{r}^{2}}}\]\[[\because E=\sigma {{T}^{4}}]\]                The area of the earth which receives this energy is only one-half of total surface area of the earth, whose projection would be\[\pi r_{0}^{2}\]. \[\therefore \]Total radiant power as received by the earth \[=\pi r_{0}^{2}\times I=\frac{\pi r_{0}^{2}\times \sigma {{R}^{2}}{{T}^{4}}}{{{r}^{2}}}=\frac{\pi r_{0}^{2}{{R}^{2}}\sigma {{T}^{4}}}{{{r}^{2}}}\]