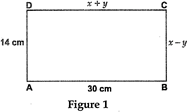
| In fig. 1, ABCD is a rectangle. Find the values of x and y. |
 |
| Two different dice are tossed together. Find the probability: |
| (i) of getting a doublet |
| (ii) of getting a sum 10, of the numbers on the two dice. |
| An integer is chosen at random between 1 and 100. Find the probability that it is: |
| (i) divisible by 8. |
| (ii) not divisible by 8. |
| If \[A\,(-2,1,)\text{ }B\,(a,0,\text{ }C\text{ (}4,b)\] and \[D\text{ (}1,2)\] are the vertices of a parallelogram ABCD, find the values of a and b. Hence find the lengths of its sides. |
| OR |
| If \[A\,(-5,7),\text{ }B\,(-4,-5),\text{ }C\text{ (}-1,-6)\] and \[D\text{ (}4,5)\]are the vertices of a quadrilateral, find the area of the quadrilateral ABCD. |
| Prove that the area of an equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonal. |
| OR |
| If the area of two similar triangles are equal, prove that they are congruent. |
| If \[4\text{ }tan\text{ }\theta =3\], evaluate \[\left( \frac{4\,\,\sin \,\,\theta -\cos \,\,\theta +1}{4\,\,\sin \,\,\theta +\cos \,\,\theta -1} \right)\] |
| OR |
| If tan \[2A=cot\text{ (}A-18{}^\circ )\], where 2A is an acute angle, find the value of A. |
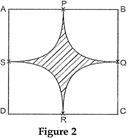
| Find the area of the shaded region in Fig. 2, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm, [Use \[\pi =3.14\]] |
 |
| A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 3. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm. Find the article. |
 |
| OR |
| A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap? |
| The table below shows the salaries of 280 persons: | |
| Salary (In thousand Rs.) | No. of Persons |
| 5 ? 10 | 49 |
| 10 ? 15 | 133 |
| 15 ? 20 | 63 |
| 20 ? 25 | 15 |
| 25 ? 30 | 6 |
| 30 ? 35 | 7 |
| 35 ? 40 | 4 |
| 40 ? 45 | 2 |
| 45 ? 50 | 1 |
| Calculate the median salary of the data. | |
| A motor boat whose speed is 18 km/hr. in still water takes 1 hr. more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream. |
| OR |
| A train travels at a certain average speed for a distance of 63 km and then travels at a distance of 72 km at an average speed of 6 km/hr. more than its original speed. If it takes 3 hours to complete total journey, what is the original average speed? |
| In an equilateral \[\Delta \text{ }ABC,\text{ }D\]is a point on side BC such that \[BD=\frac{1}{3}BC\]. Prove that \[9{{(AD)}^{2}}\] \[=7{{(AB)}^{2}}\]. |
| OR |
| Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides. |
| The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find: |
| (i) The area of the metal sheet used to make the bucket. |
| (ii) Why we should avoid the bucket made by ordinary plastic? [Use \[\pi =3.14\]] |
| The mean of the following distribution is 18. Find the frequency f of the class 19 ? 21. | |||||||||||
| Class | 11 ? 13 | 13 ? 15 | 15 ? 17 | 17 ? 19 | 19 ? 21 | 21 ? 23 | 23 ? 25 | ||||
| Frequency | 3 | 6 | 9 | 13 | f | 5 | 4 | ||||
| OR | |||||||||||
| The following distribution gives the daily income of 50 workers of a factory: | |||||||||||
| Daily Income (in Rs.) | 100 ? 120 | 120 ? 140 | 140 ? 160 | 160 ? 180 | 180 ? 200 | ||||||
| Number of workers | 12 | 14 | 8 | 6 | 10 | ||||||
| Convert the distribution above to a less than type cumulative frequency distribution and draw it?s give. | |||||||||||
You need to login to perform this action.
You will be redirected in
3 sec
